Помогите решить!

упростить: (sin10x+sin6x+sin2x)/(cos6x+cos6x+cos2x)

NNNLLL54: (cos6x+cos6xcos2x)=2cos6x+cos2x ...? может, (cos10x+cos6x+cos2x) ? уточни условие...

dilshodbekatanazarov: надо просто упростить!

NNNLLL54: это понятно, проверь , что записано в знаменателе

dilshodbekatanazarov: не понел что за "знаменателе"

NNNLLL54: знаменатель - это знаменатель... это ещё в 3 классе учат

dilshodbekatanazarov: спасибо за ответ 1 (вариант ответа более подходяший)

NNNLLL54: ты ошибся, наверное, в записи знаменателя, о чём я тебя пыталась спросить...

dilshodbekatanazarov: в вопросе так инаписано

dilshodbekatanazarov: было

dilshodbekatanazarov: но варианты ответов были такие "A) cos2a B) 2 C) tg6a D) sin10a"

Ответы

Ответ дал: xgamerxpowerp9qy5j

Ответ:

на фото.......

Объяснение:

Приложения:

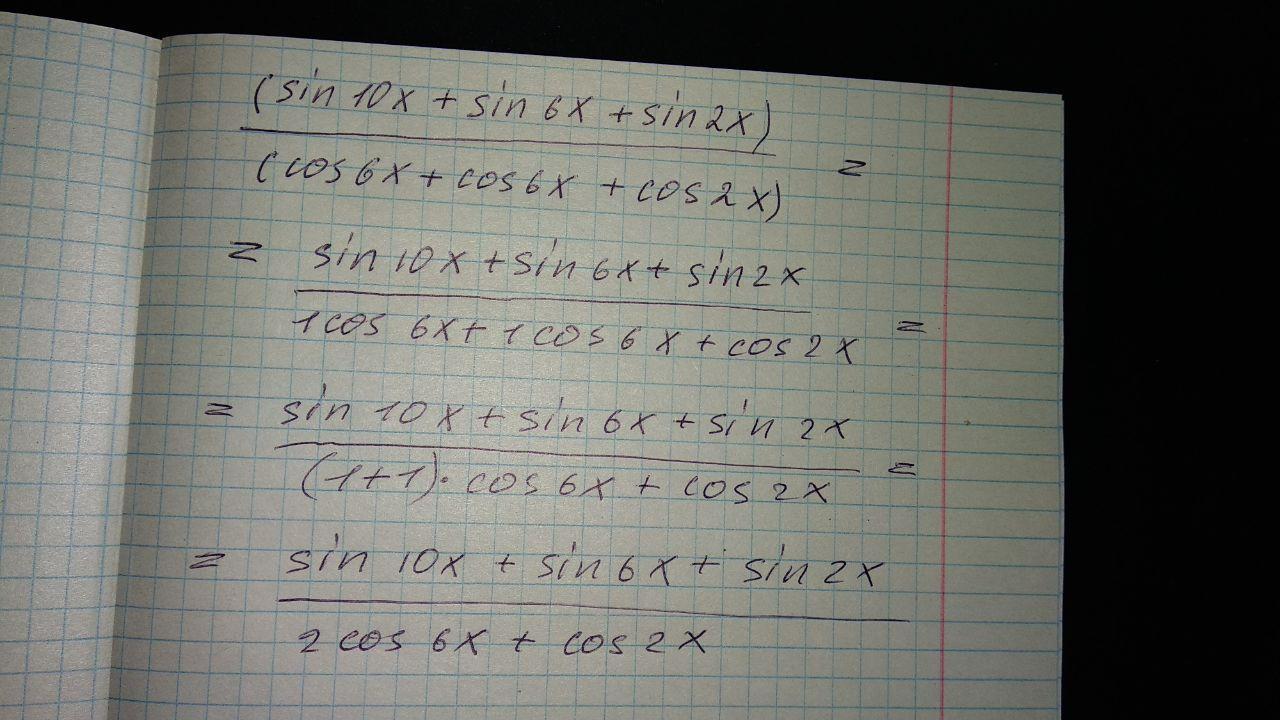
dilshodbekatanazarov: это же не окончательный ответ

Ответ дал: NNNLLL54

$\dfrac{sin10x+sin6x+sin2x}{cos10x+cos6x+cos2x}=\dfrac{2\, sin6x\cdot cos4x+sin6x}{2\, cos6x\cdot cos4x+cos6x}=\\\\\\=\dfrac{sin6x(2cos4x+1)}{cos\, 6x(2cos4x+1)}=\dfrac{sin6x}{cos\, 6x}=tg6x$

$\star \ \ \ \dfrac{sin10x+sin6x+sin2x}{cos6x+cos6x+cos2x}=\dfrac{sin6x(2cos4x+1)}{2cos6x+cos2x}=\\\\=\dfrac{sin6x(2cos4x+1)}{2(4cos^32x-3cos2x)+cos2x}=\dfrac{sin6x(2cos4x+1)}{8cos^32x-5cos2x}=\dfrac{sin6x(2cos4x+1)}{cos2x(8cos^22x-5)}$