Question

Стоя вертикально ясным солнечным днём, вы обнаружили, что длина вашей тени в два
раза меньше вашего роста. На какой высоте над горизонтом находится солнце

Answer 1

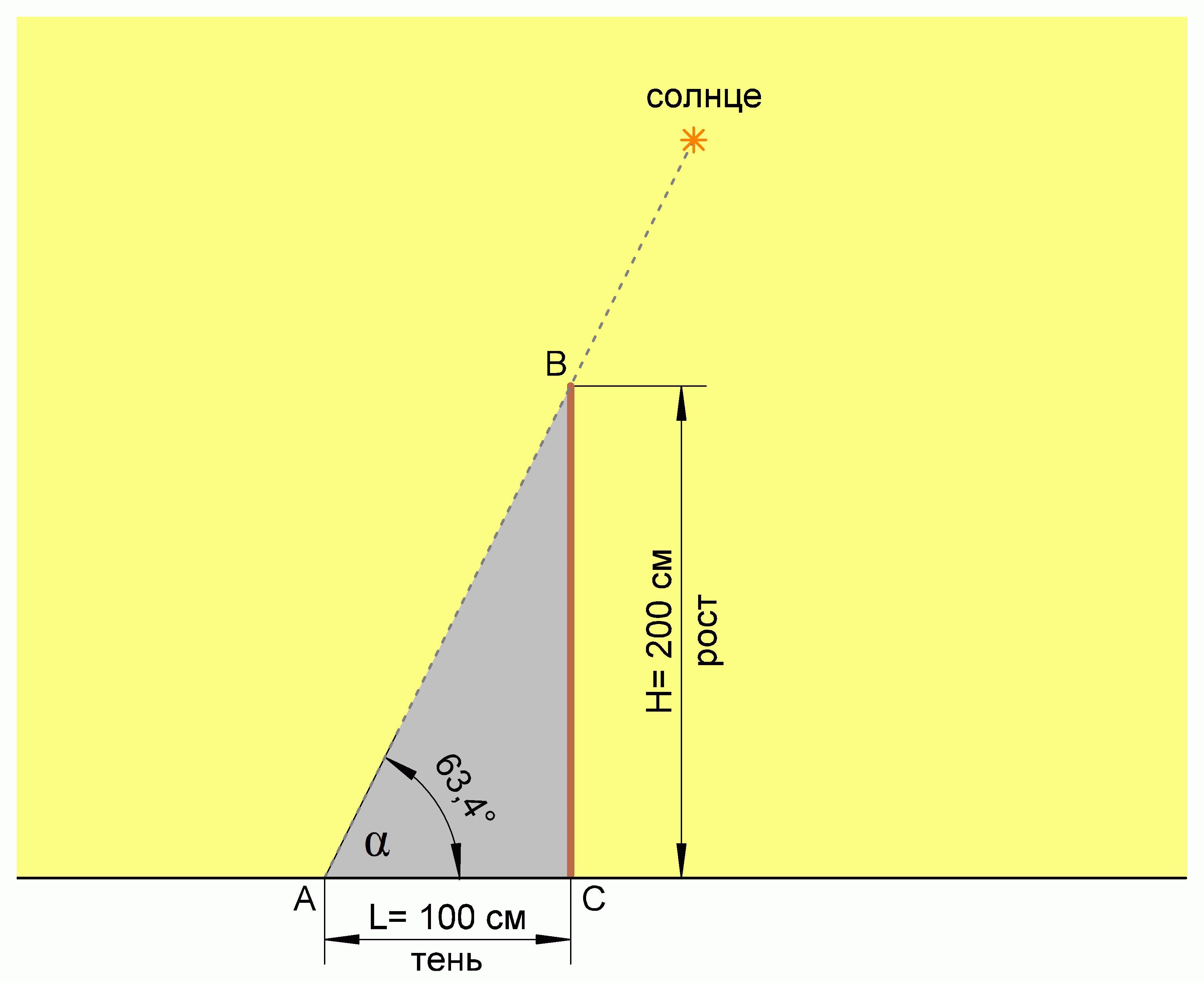
В прямоугольном треугольнике ABC (см.рисунок), тангенс угла  $\alpha$ равен отношению противолежащего катета к прилежащему.

То есть, высоту роста (H) делим на длину тени (L)

А по условиям задачи рост в два раза больше тени (H = 2L)

$\mathrm{tg}\, \alpha=\frac{H}{L}=\frac{2L}{L}=2$

Отсюда, находим сам угол  $\alpha$

$\alpha= \operator{arctg} \, 2 \approx 63,4 \textdegree$

Ответ: высота (т.е. угол) солнца над горизонтом  $\alpha \approx 63,4 \textdegree$