Исследовать числовой ряд на сходимость и указать название используемого при этом признака:
Приложения:
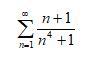
Ответы
Ответ дал:
0
Ответ: ряд сходится, при решении задачи использован признак сравнения.
Пошаговое объяснение:
Сравним это ряд с рядом обратных квадратов ∑1/n², который, как известно, сходится. Для этого составим разность 1/n²-(n+1)/(n⁴+1)=(n⁴-n³-n²+1)/[n²*(n⁴+1)]. Так как знаменатель этой дроби положителен при любом n, то её знак будет зависеть от знака числителя n⁴-n³-n²+1. Но n⁴-n³-n²+1=n²*[(n-1/2)²-5/4]+1=n²*(n-1/2)²-5/4*n²+1. Отсюда следует, что числитель обращается в ноль лишь при n=1; если же n>1, то он положителен, а это значит, что при n>1 1/n²>(n+1)/(n⁴+1). Поэтому данный ряд сходится.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад