Дана равнобедренная трапеция ABCD. AB – большое основание трапеции и на ней взята точка E так, что угол ∠DEC стал равным углу при основании трапеции. Если DE=6, EC=10, найдите отношение длины отрезка BE к длине отрезка AE. (ответ 9/25)
Kierra:
У меня наоборот, 25:9 получается...
все равно спасибо, может хоть так пойму
Ответы
Ответ дал:
3
Дано: ABCD — трапеция, ВС=AD, АВ||CD, т.Е∈АВ;
∠СВА=∠DAE=∠DEC, DE=6, EC=10.
Найти: ВЕ:АЕ.
Решение.
∠СВА=∠DAE=∠DEC=α.
∠DEA=∠CDE=β как накрест лежащие при секущей ED и AB||CD.
∠BEC=∠ECD=γ как накрест лежащие при секущей ЕС и AB||CD.
Прямая АВ, т.Е лежит на ней. ∠ВЕС+∠CED+∠DEA=180°.
В ΔCBE: ∠CBA=α, ∠BEC=γ, ∠ВСЕ=β.
В ΔEDC: ∠DEC=α, ∠CDE=β, ∠ECD=γ.
В ΔEAD: ∠DAE=α, ∠DEA=β, ∠EDA=γ.
Треугольники СВЕ, EDC и EAD подобны (по трем углам)
Значит, их соответственные стороны относятся.
Пусть BC=AD=x.
Через подобные треугольники СВЕ и EAD найдем (выразим) стороны ВЕ и АЕ.
1) ВЕ/AD=CE/ED;
BE/x= 10/6;
BE= 10x/6;
BE= 5x/3.
2) BC/AE=CE/ED;
x/AE= 10/6;
AE= 6x/10;
AE= 3x/5.
BE:AE= 5x/3 : 3x/5 = 5x/3 • 5/3x= 25x/9x= 25:9.
Ответ: ВЕ:АЕ=25:9.
Приложения:
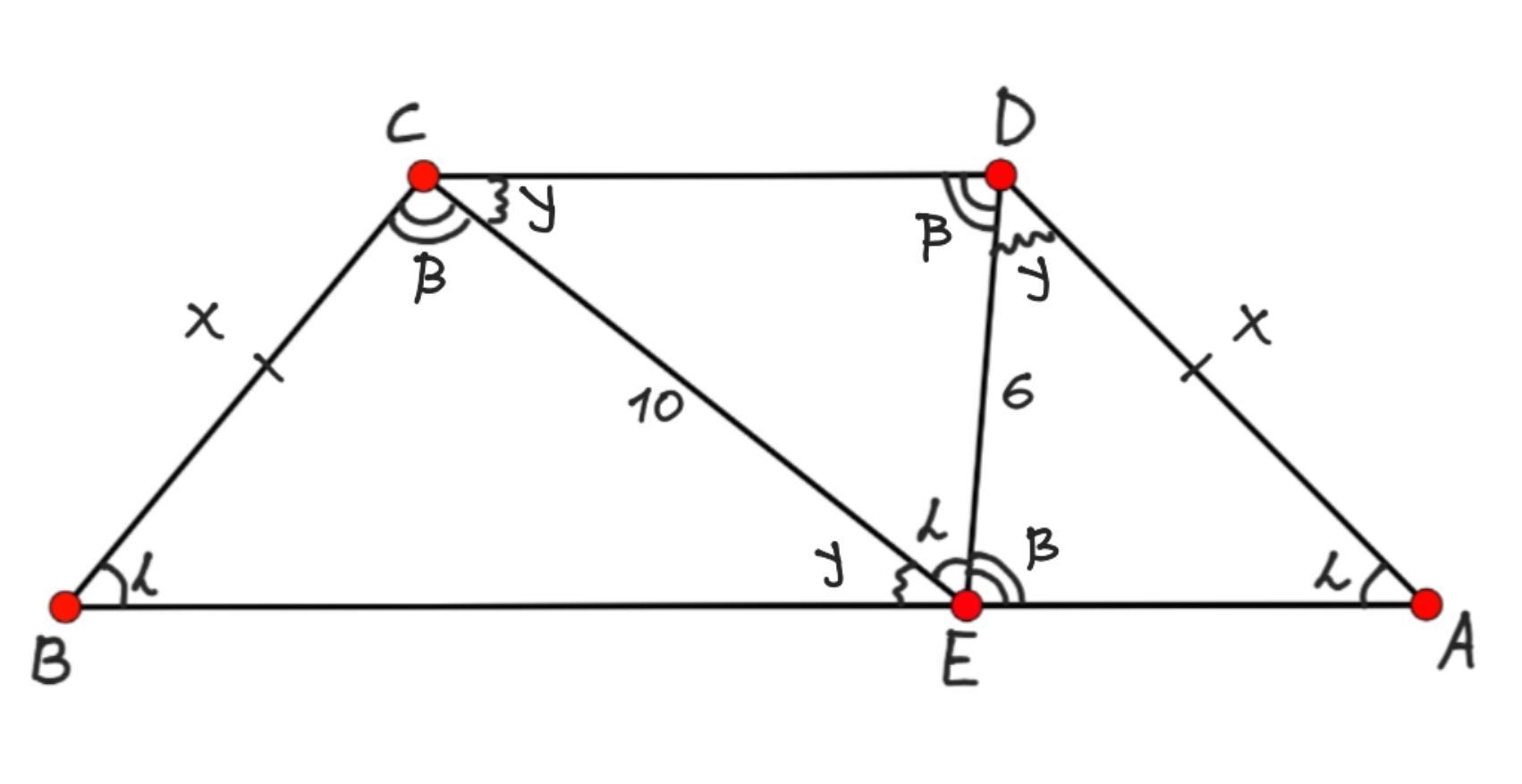
Треугольник ВСЕ имеет более длинные стороны, чем AED, поэтому стороны ВЕ и АЕ относиться 9:25 в принципе не могут
Только наоборот)
у меня в тестах были ошибки, наверное, это одна из них
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад