Докажите, что перпендикуляр, проведëнный из точки пересечения диагоналей прямоугольника ABCD к прямой AB, является средней линией треугольника ABC.
Ответы
Ответ дал:
8
Решение:
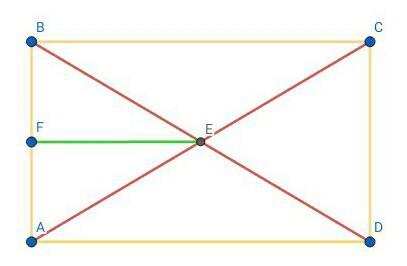
1)Отметим пересечение диагоналей прямоугольника ABCD точкой Е.
Проведём из точки Е перпендикуляр (или высоту) EF к прямой АВ.
Диагонали прямоугольника равны.
=> BD = AC.
Диагонали прямоугольника делятся точкой пересечения пополам.
=>АЕ = EC = ED = BE.
Из этого =>, что △ВЕА - равнобедренный (АЕ = ЕВ)
Высота, проведённая из вершины равнобедренного треугольника к основанию равнобедренного треугольника, является медианой и биссектрисой.
=> ВF = FA, так как FE - медиана.
2)Так как BF = FA, AE = EC => F и Е - середины АС и АВ.
3) Из 2) =>, что FE - средняя линия △АВС.
Ч.Т.Д.
Приложения:
fedorr2005:
спасибо
Здравствуйте, не за что, обращайтесь, если что-то будет непонятно. Всего доброго и до свидания!
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад