7 класс

В треугольнике ABC проведены биссектриса AD и высота CH, причем
точка H лежит на отрезке AB. Угол DAC в 3 раза меньше угла ABC, а угол
BCH и внешний угол при вершине C относятся как 3 к 20 соответственно.
Найдите углы треугольника ABC

Без спама, пожалуйста.
Очень надо :‹

planpeace: Точно 3 к 20? А то углы получаются дробные

Ответы

Ответ дал: vikll

Ответ:

Объяснение:В треугольнике ABC проведены биссектриса AD и высота CH, причем

Приложения:

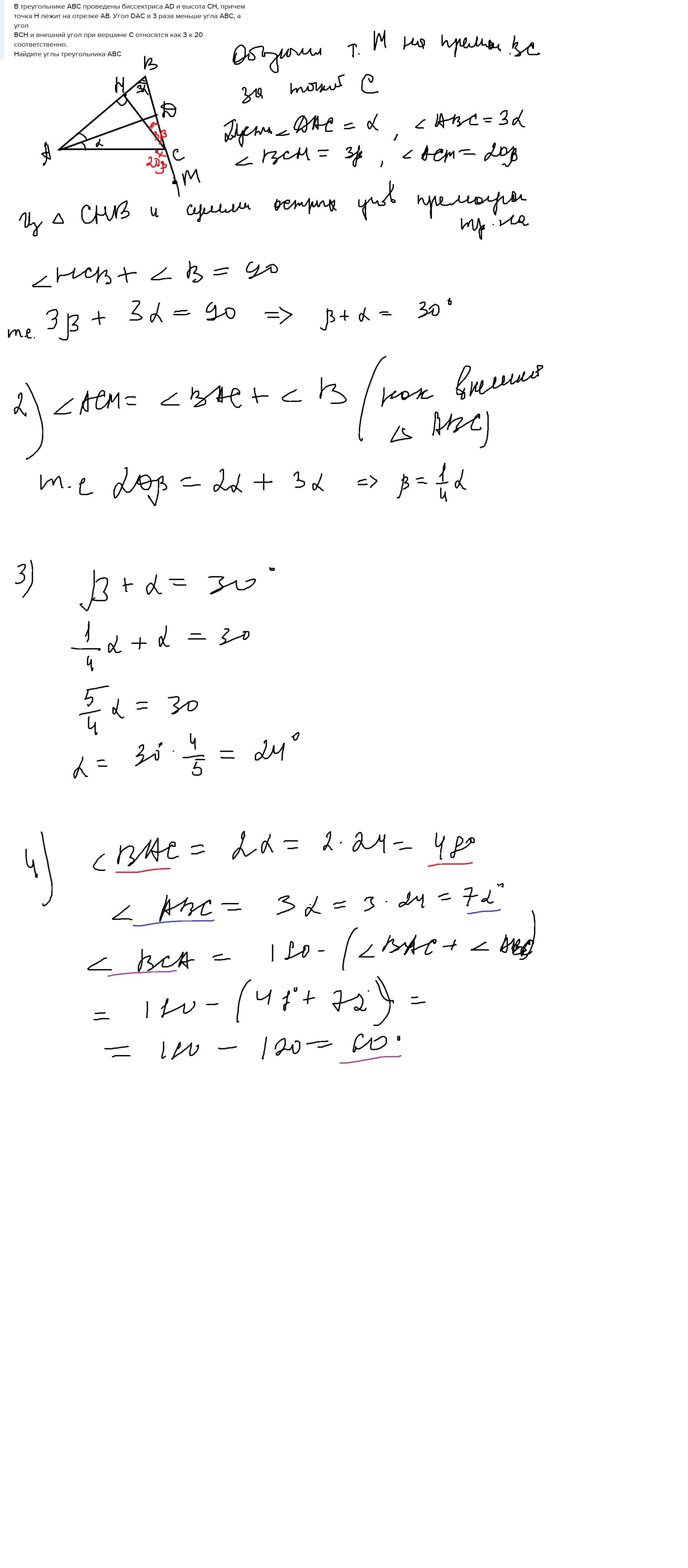
MandarinDarin: Уф, прости, сложновато разобрать.

vikll: Пусть ∠DАС=х⇒∠ABC=3х, а∠ВАС=2х(т.к.АD-биссекетрисса). И обозначим ∠BCH = 3у⇒внешний угол при вершине C равен 20у. Из ∆СНВ и суммы острых углов прямоугольного тр-ка: ∠BCH+∠ABC=90 т.е.3х+3у=90. А ∠АСМ=∠ВАС+∠ABC(как внешний∆ АВС)т.е. 2х+3х=20у

Вас заинтересует

История

2 года назад

Помогите пожалуйста решить задания с 1 по 6

История

2 года назад

Назовите правителя кыпчакского государства пжжжжжжж

Английский язык

2 года назад

загадки англиского языка проигрушку

Русский язык

2 года назад