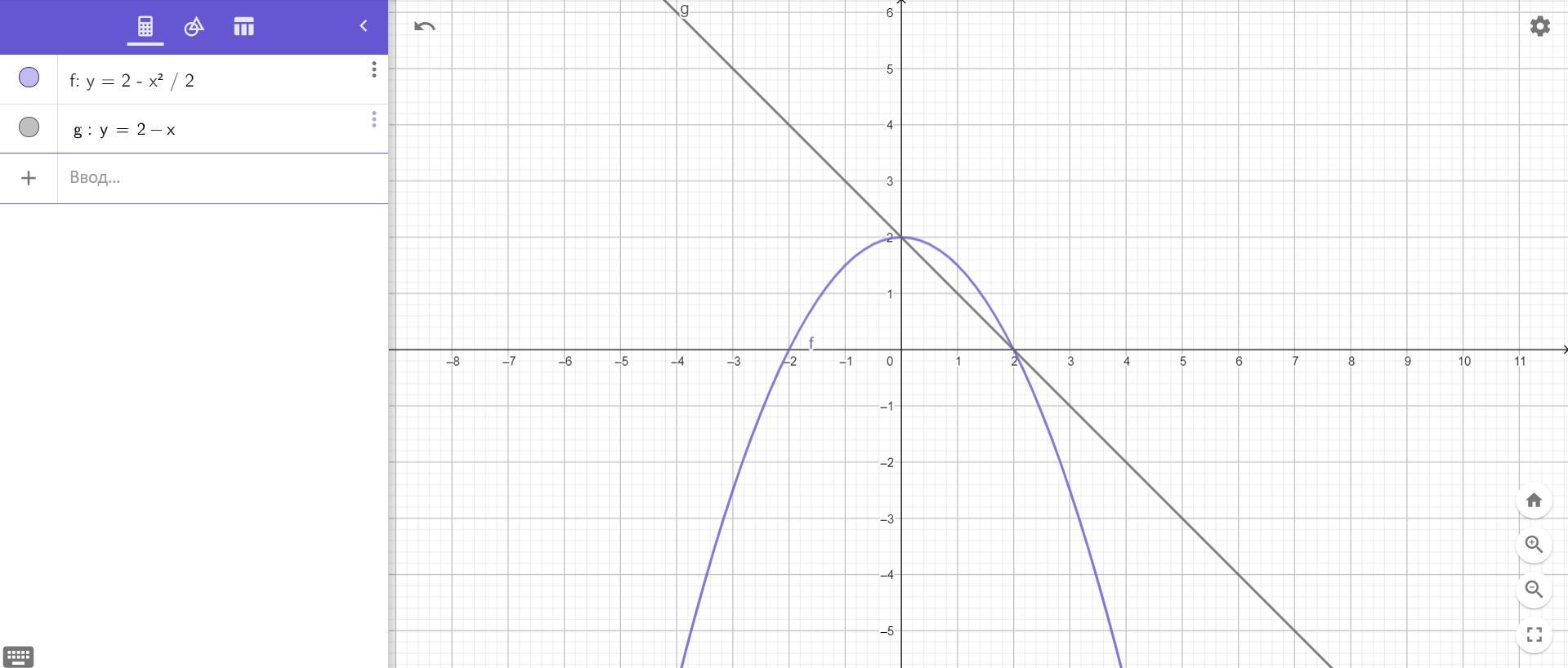
определить объем тела, образованного вращением вокруг оси OY фигуры, ограниченной линиями
если график неверный, то приложите, пожалуйста

Приложения:
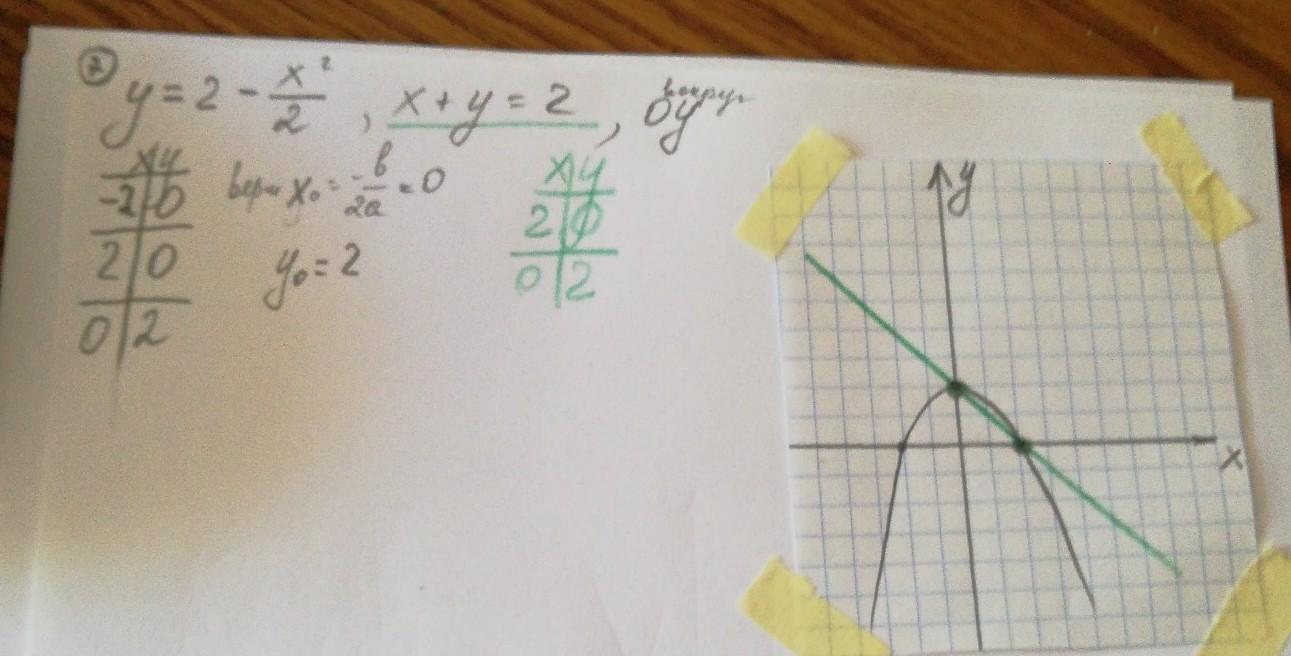
Ответы
Ответ дал:
1
Видно, что для объема нам нужно взять первый график с "+". Тогда имеем:
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад