Question

помогите пожалуйста, тема:"свойства биссектрисы треугольника"​

Answer 1

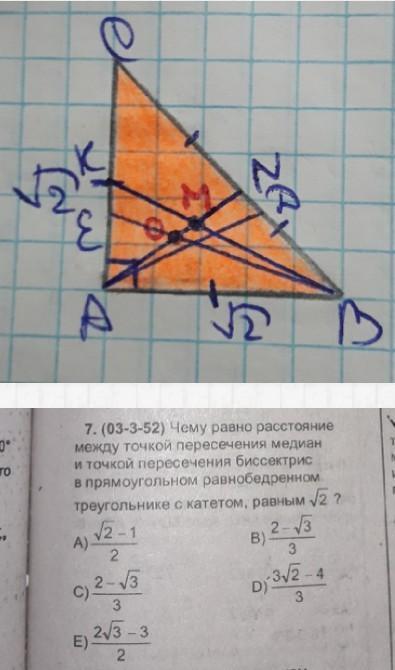
Картинка странная - ведь в равнобедренном треугольнике медиана, биссектриса (а заодно и высота), опущенные на основание, совпадают. То есть на картинке точки O и M совпадают.

Сначала находим по теореме Пифагора гипотенузу: BC=2. Поэтому CN=NB=AN=1, а поскольку медианы точкой пересечения делятся в отношении 2:1, считая от вершины, MN=1/3.

Далее, биссектриса делит сторону на отрезки, пропорциональные боковым сторонам. Применяя эту теорему к треугольнику ABN, получаем  $\frac{AO}{ON}=\frac{AB}{NB}=\frac{\sqrt{2}}{1};\ AO=x\sqrt{2}; ON=x; AO+ON=x(\sqrt{2}+1)=1;$

$x=\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}=\sqrt{2}-1\Rightarrow ON=\sqrt{2}-1;$

$OM=|\sqrt{2}-1-\frac{1}{3}|=\frac{3\sqrt{2}-4}{3}$

Ответ: D