Question

Площадь основания правильной четырехугольной пирамиды 16 см и

боковая поверхность 24 см в квадрате . Определить объем пирамиды.

Answer 1

Дано:

Правильная четырёхугольная пирамида.

S осн = 16 см²

S бок поверхности = 24 см²

Найти:

V - ?

Решение:

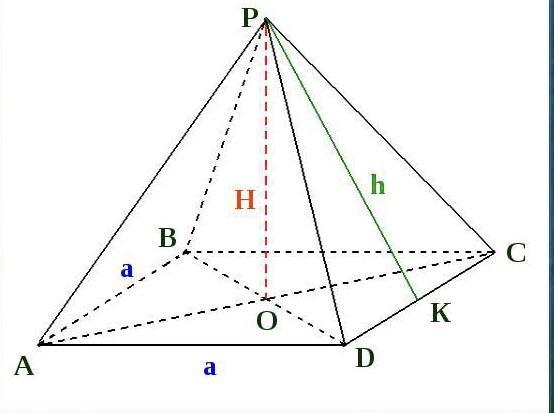
Н - высота.

h - апофема.

а - сторона основания.

"Правильный многоугольник - многоугольник, у которого все стороны и углы равны".

Так как данная пирамида - правильная, четырёхугольная => основание этой пирамиды - квадрат.

"Квадрат - геометрическая фигура, у которой все стороны равны".

S квадрата = а² = 16 см²

=> а = √16 = 4 см.

S бок поверхности = 1/2 * S квадрата * h = 2 * a * h = 24 см²

а = 4 см.

=> h = (24/2)/4 = 3 см.

ОК = 1/2а = 4/2 = 2 см.

Найдём высоту пирамиды Н, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)

а = √(c² - b²) = √(3² - 2²) = √(9 - 4) = √5 = 2,23607 ≈ 2,2 см

Итак, Н ≈ 2,2 см.

V = 1/3 * a² * H = 16/3 * 2,2 ≈ 176/15 ≈ 11,73 см^3.

Ответ: ≈ 11,73 см^3.