Ответы
Ответ дал:
0
Ответ:
4-ое задание:
Угол между векторами a(X1;Y1), b(X2;Y2) можно найти по формуле:
где a • b - скалярное произведение векторов.
Скалярное произведение векторов a и b, заданных своими координатам, находится по формуле: a•b = x1•x2 + y1•y2.
Найдем скалярное произведение векторов a=(1;0) и b(1;-1).
По формуле находим:
a•b = 1•1 + 0•(-1) = 1
Найдем модуль вектора a.
Найдем модуль вектора b.
Найдем угол между векторами:
y= 45°
Ответ дал:
0
Везде над векторами стоит черта или стрелка.
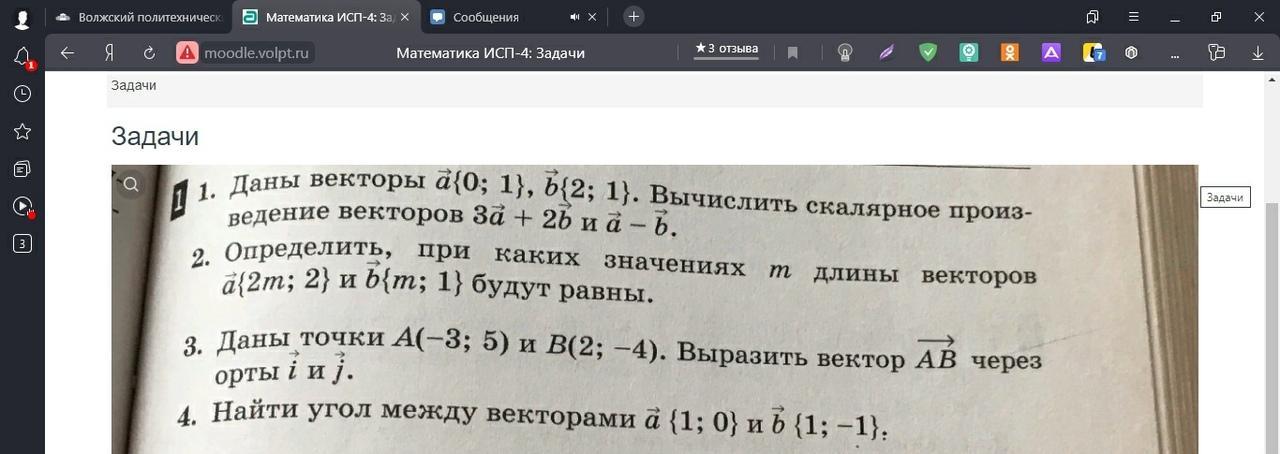
1.3а+2b=(0;3)+(4;2)=(4;5)
а-b=(-2;0)
2. Ни при каких, т.к.√( 4m²+4)≠√(m²+1);√( 4m²+4)=2*√(m²+1)
3. АВ=(5;-9)=5i-9j
4. 1*1+0*(-1)=1, значит, угол равен 0°
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад