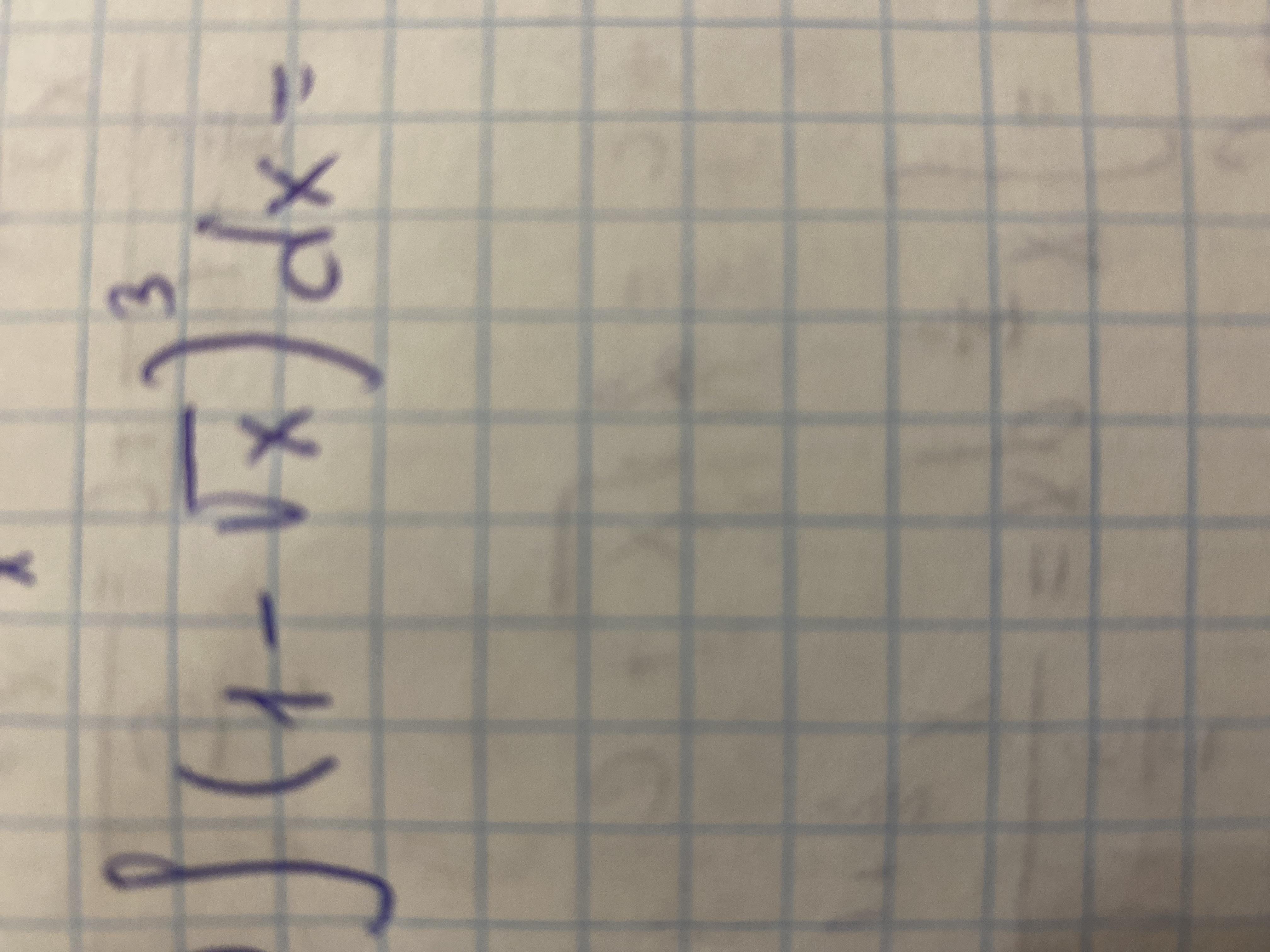Предмет: Алгебра
Автор: calvinkleinn
Вопрос задан 3 года назад

Вычислить интеграл) заранее спасибо))

Приложения:

Ответы

Ответ дал: dimb0r22

$\int\limits (1-\sqrt{x})^{3}dx = \int\limits((1-\sqrt{x})(1-\sqrt{x})(1-\sqrt{x}))dx = \\\int\limits(1-3\sqrt{x}+3x-x\sqrt{x})dx = x-2x\sqrt{x}+\frac{3x^{2}}{2}-\frac{2x^{2}\sqrt{x}}{5}+C;$

$C$ ∈ $R$ ;

Аноним: потеряли тройку

dimb0r22: Уверен, что ответил правильно:
∫(3*√(x))dx = ∫(3*(x^(1/2)))dx = 2*x^(3/2) = 2*x*√(x)
Легко проверить через выражения производной от 2*x*√(x):
(2*x*√(x))' = (2*x^(3/2))' = 2*(3/2)*x^((3/2)-1) = 3*x^(1/2) = 3*√(x)

dimb0r22: ***выражение

dimb0r22: Простите

Аноним: да нет. это Вы меня простите.

dimb0r22: Что Вы, не извиняйтесь. Я уверен, Вы просто допустили опечатку или случилось что-то подобное. Мы люди, все мы ошибаемся маленько ))

Ответ дал: Аноним

=∫(1-3√х+3х-х³/²)dx=х-(2х³/²)/3+3х₂/2-(2/5)х⁵/²+с

Вас заинтересует

Биология

2 года назад

Сообщение о «Шляпочных грибах» за 5 класс :)

Литература

2 года назад