Question

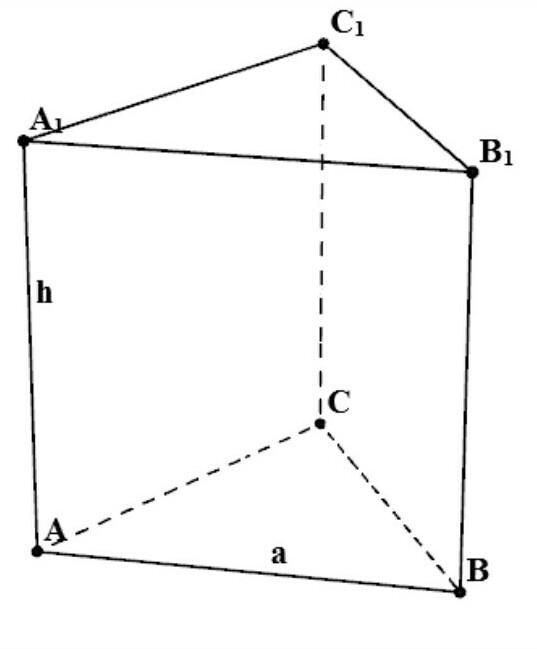
Якщо в правильній трикутній призмі бічне ребро дорівнює 12 см, а сторона основи 10 см, то площа поверхні призми дорівнює

Answer 1

Дано:

Правильная треугольная призма.

АА1 = 12 см

АВ = 10 см

Найти:

S полной поверхности - ?

Решение:

Так как данная призма - треугольная, правильная => основание данной призмы - равносторонний треугольник.

Равносторонний треугольник - треугольник, у которой все стороны и углы равны.

=> АВ = ВС = АС = 10 см

S боковой поверхности = Рh, где Р - периметр основания; h - высота призмы.

Р = AB + BC + AC = 3 * 10 = 30 см

h = AA1 = 12 см.

S боковой поверхности = 30 * 12 = 360 см²

S равностороннего △ = а²√3/4, где а - сторона треугольника.

S равностороннего △ = 10²√3/4 = 25√3 см²

S полной поверхности = S боковой поверхности + 2S основания = 360 + (2 * 25√3) = 10(36 + 5√3) см²

Ответ: 10(36 + 5√3) см²