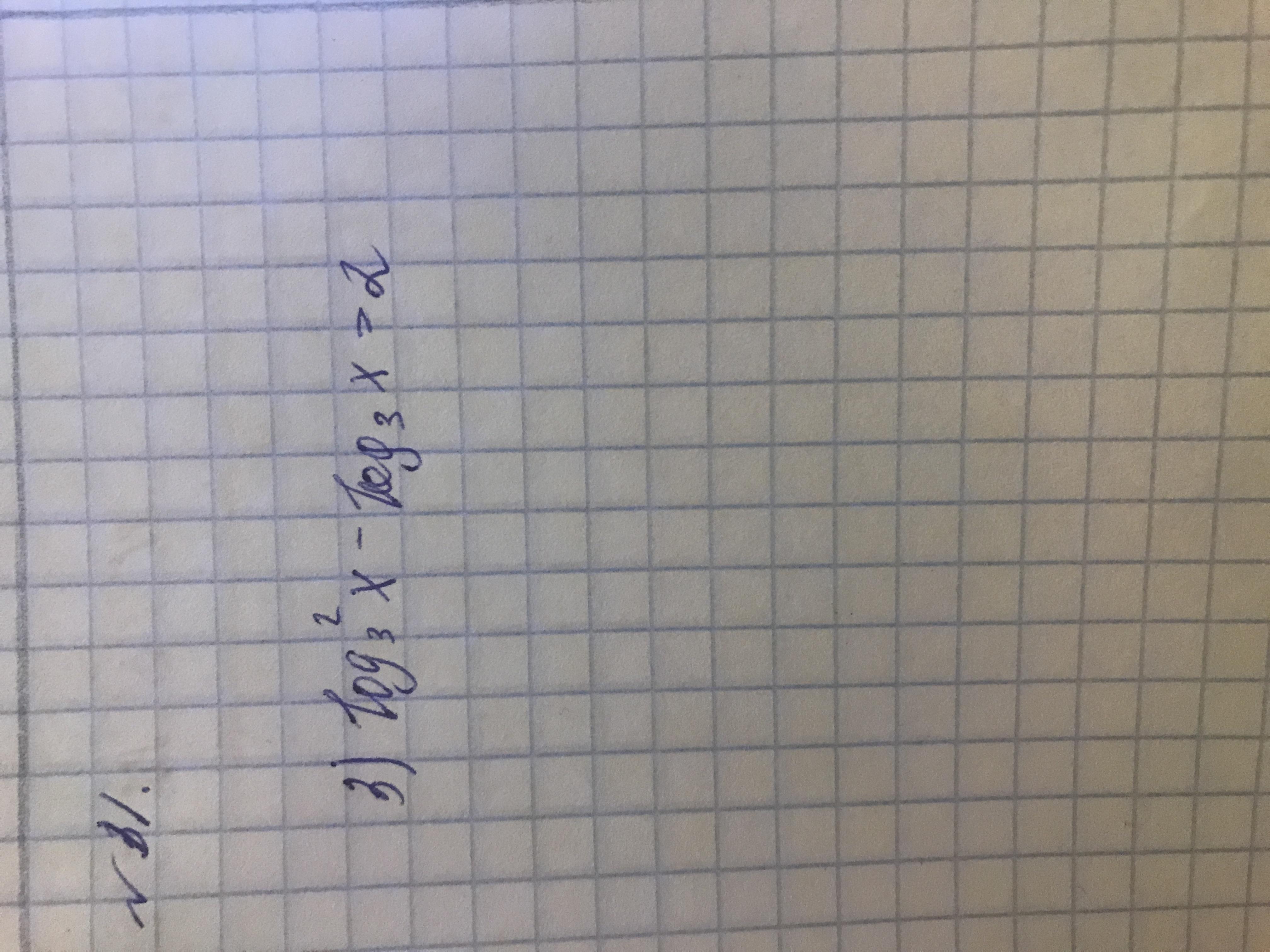Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
Приложения:
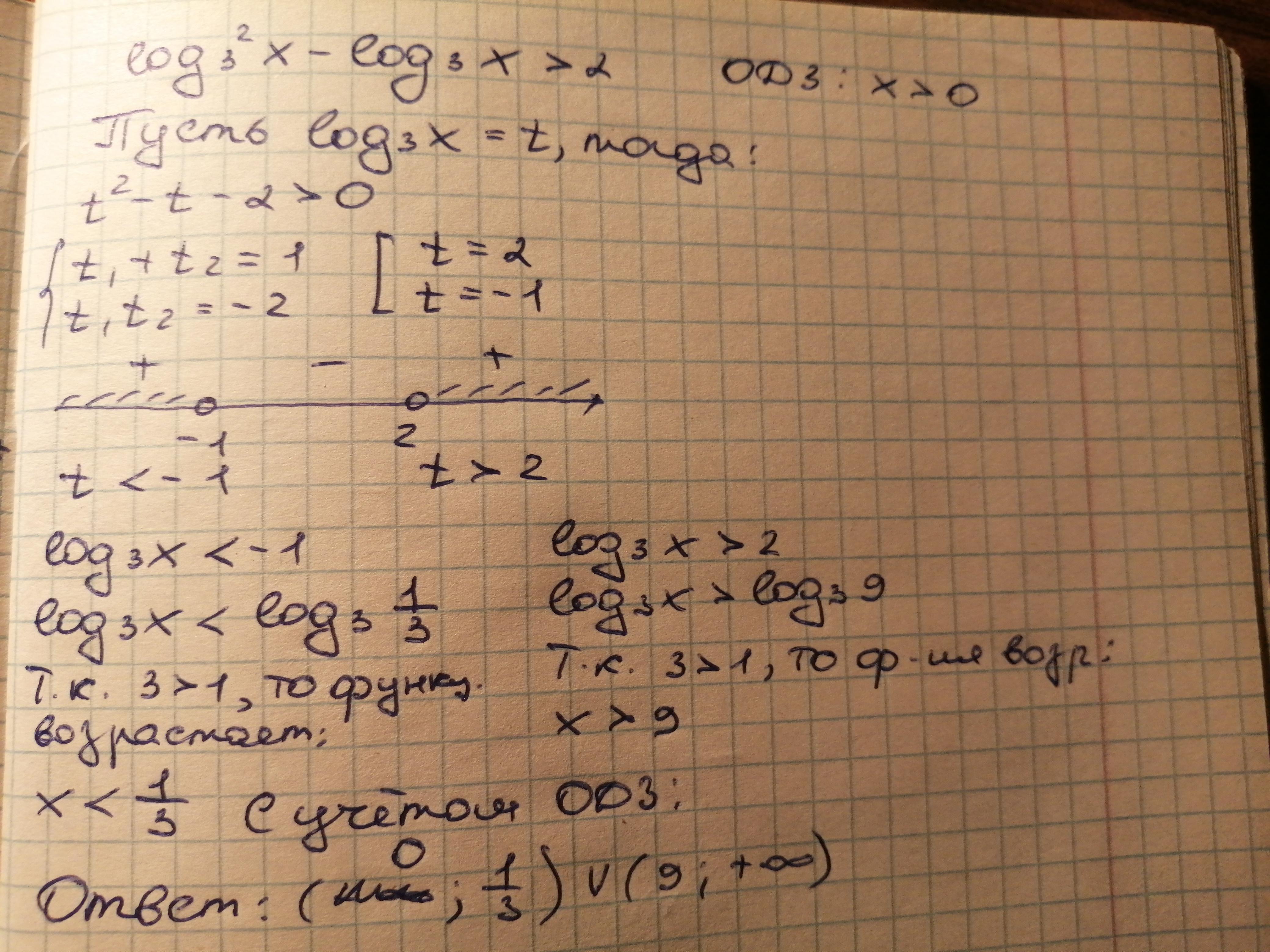
dpenkina:
спасибо конечно,но там стоит равно,а не знак больше,немного не корректно написалаъ
Так как x находится под знаком логарифма, то на него накладывается ограничение x>0, а он у вас все отрицательные значения вместе с нулем захватил, что является наигрубейшей ошибкой
Я это исправил, действительно я сначала забыли
Про одз
Ответ дал:
0
Ответ:
∈(0;
)∪(9;+∞)
Пошаговое объяснение:
, пусть
, тогда наше неравенство принимает вид:
⇒
⇒
∈(-∞;-1)∪(2;+∞), ⇒
∈(-∞;-1)∪(2;+∞) ⇒
∈(0;
)∪(9;+∞)
Ответ: ∈(0;
)∪(9;+∞)
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад