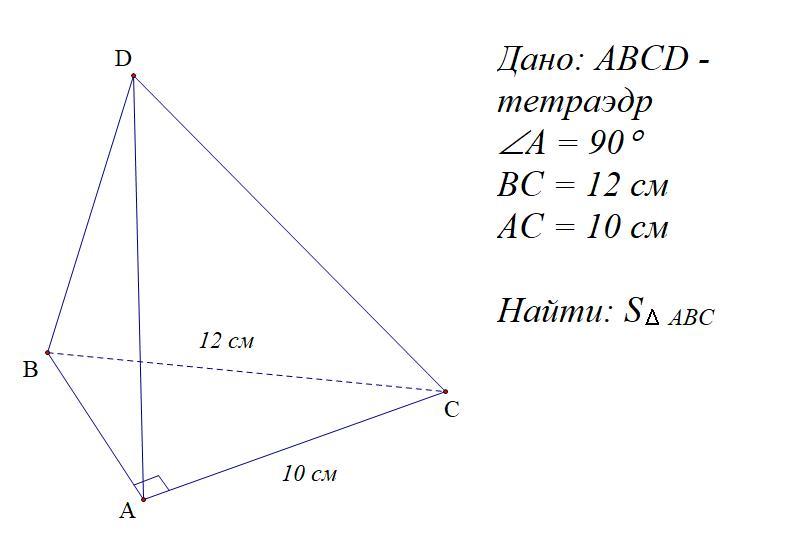
В основании тетраэдра прямоугольный треугольник, гипотенуза которого равна 12 см. Один из катетов имеет длину 10 см. Найти площадь основания тетраэдра.
Ответы
Ответ дал:
1
Ответ: 10√11 см².
Объяснение:
Так как ΔABC -- прямоугольный, то справедлива теорема Пифагора:
BC² = AB² + AC²
12² = AB² + 10²
AB² = 144 - 100
AB = √44 см
AB = 2√11 см
Площадь прямоугольного треугольника равна полупроизведению его катетов, имеем:
SΔABC = 1/2 * AB * AC = 1/2 * 2√11 * 10 = 10√11 см²
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад