Question

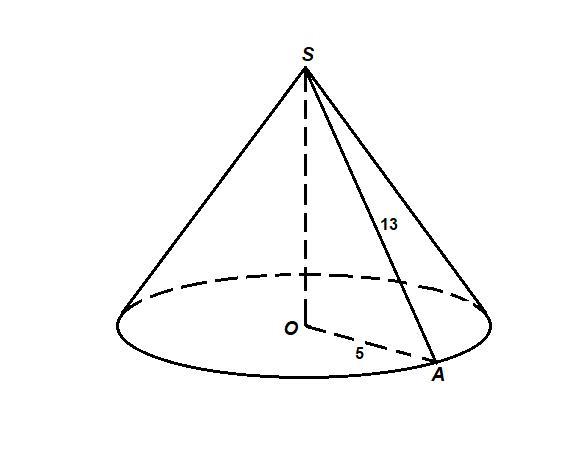
Радиус основания конуса равен 5 см, а образующая конуса равна 13 см. Найдите объём конуса, и площадь полной поверхности.

Answer 1

Ответ:

V = 100π см³

S = 90π cм²

Объяснение:

Образующая, радиус основания  и высота  образуют прямоугольный треугольник SOA.

По теореме Пифагора:

$SO=\sqrt{SA^2-OA^2}=\sqrt{13^2-5^2}=\sqrt{169-25}=\sqrt{144}=12$ см

Объем конуса:

$V=\dfrac{1}{3}\pi r^2h$

где r = OA = 5 см,  h = SO = 12 см.

$V=\dfrac{1}{3}\pi \cdot 5^2\cdot 12=4\cdot 25\cdot \pi =100\pi$ см³

Площадь полной поверхности конуса:

$S=\pi rl+\pi r^2$

где $l$ = SA = 13 см

$S=\pi \cdot 5\cdot 13+\pi \cdot 5^2=65\pi +25\pi =90\pi$ см²