Помогите, пожалуйста, решить
Приложения:
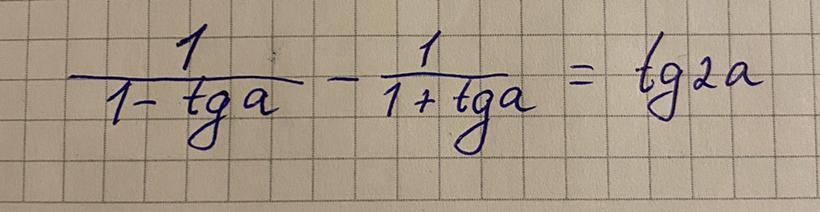
Tanda80:
Решить или доказать тождество?
Доказать
Доброй ночи) Вы можете помочь мне с симплекс-методом?
доброй! маловероятно. :( Извините
Ответы
Ответ дал:
1
Доказать, что
Доброй ночи) Вы можете помочь мне с симплекс-методом?
Ответ дал:
1
Поработаем с левой частью
Как известно
Доказано
Доброй ночи) Вы можете помочь мне с симплекс-методом?
Здравствуйте. К сожалению, нет
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад