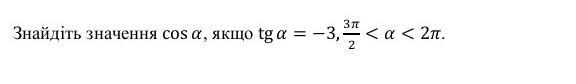Ответы
Ответ дал:
1
Ответ:
Объяснение:
Universalka:
Косинусы углов четвёртой четверти положительны
Уберите минус из ответа
Да, вы правы, перепутала с синусом. Спасибо за исправление!
Ответ дал:
0
α - угол четвёртой четверти значит Cosα > 0 .
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад