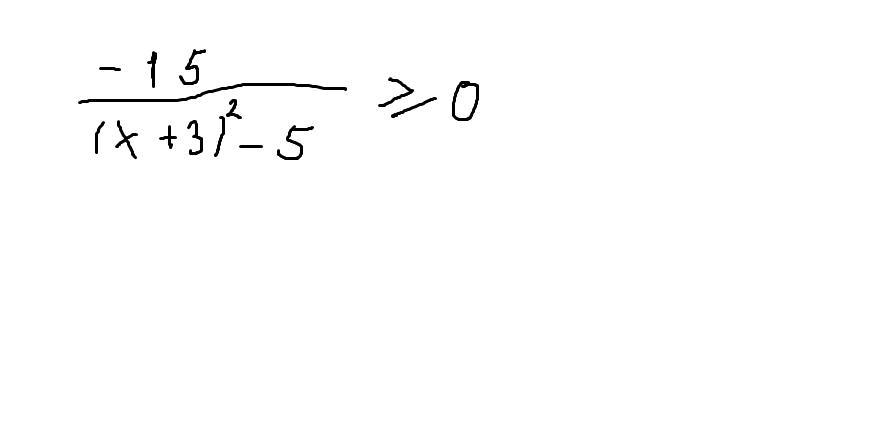Ответы
Ответ дал:
1
Ответ:
Объяснение:
-15/(x+3)²-5≥0
(x+3)²-5=0
x²+6x+9-5=0
x²+6x+4=0
D=36-16=20
D=√20=2√5
x=(-6±2√5)/2= -3±√5
- ----- ++++ ------
---------------- (-3-√5)-----------------(-3+√5)--------------
x∈(-3-√5 ; -3+√5)
Ответ дал:
0
Т.к. у нас дробь ≥0, а числитель отрицателен ⇒знаменатель тоже отрицателен
x²+6x+4=0
D = 6² - 4*4 = 36 - 16 = 20 = (2√5)²
Ответ: х∈( -3-√5 ; -3+√5)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад