Найти наибольшее и наименьшее значение функции. Пожалуйста, напишите подробный ответ.
Приложения:
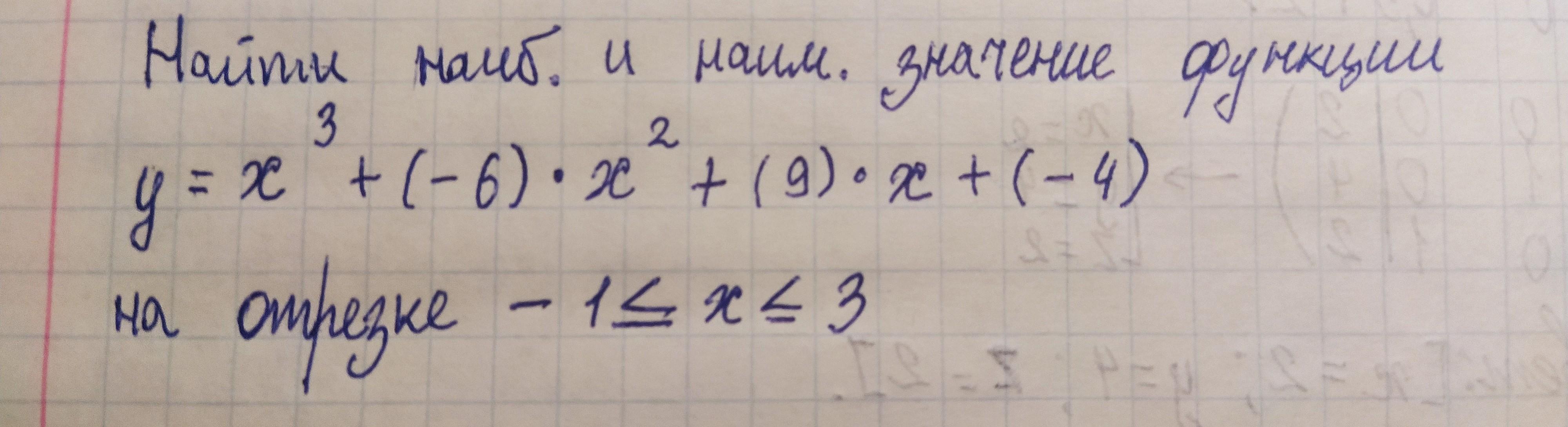
Ответы
Ответ дал:
1
y = x³ - 6x² + 9x - 4
Найдём производную :
y' = (x³ - 6x² + 9x - 4)' = (x³)' - 6(x²)' + 9(x)' - 4' = 3x² - 12x + 9
Приравняем производную к нулю, найдём критические точки :
3x² - 12x + 9 = 0
x² - 4x + 3= 0
По теореме Виета :
x₁ = 1 x₂ = 3
Обе точки принадлежат заданному отрезку .
Найдём значения функции в критических точках и на концах отрезка и сравним их :
y(1) = 1³ - 6 * 1² + 9 * 1 - 4 = 1 - 6 + 9 - 4 = 0
y(3) = 3³ - 6 * 3² + 9 * 3 - 4 = 27 - 6 * 9 + 27 - 4 = 54 - 54 - 4 = -4
y(-1) = (- 1)³ - 6 * (- 1)² + 9 * (- 1) - 4 = - 1 - 6 - 9 - 4 = - 20
Ответ : наибольшее значение функции равно 0 , а наименьшее значение равно ( - 20) .
Sally86:
В ответах написано, что там [0; -20]... Я точно правильно переписала задание, 10 раз проверила...
Вы правы, я пропустила в одном месте квадрат . Исправила .
Спасибо... Вы спасли меня!
Хорошо, что не подвела :) Всегда рада помочь.
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад