Ответы
Ответ дал:
2
Такие задачи часто решаются при помощи формулы Ньютона-Лейбница:
В данном случае (результат приравнивая функций
и
),
(соответствует заданная в условии линия
) и
(линия
).
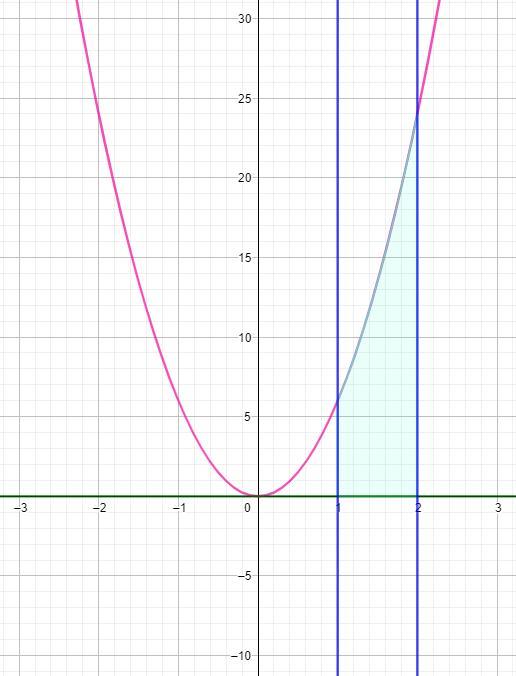
То есть, площадь искомой фигуры равна (ед²). Рисунок смотрите ниже, в приложении.
Задача решена!
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад