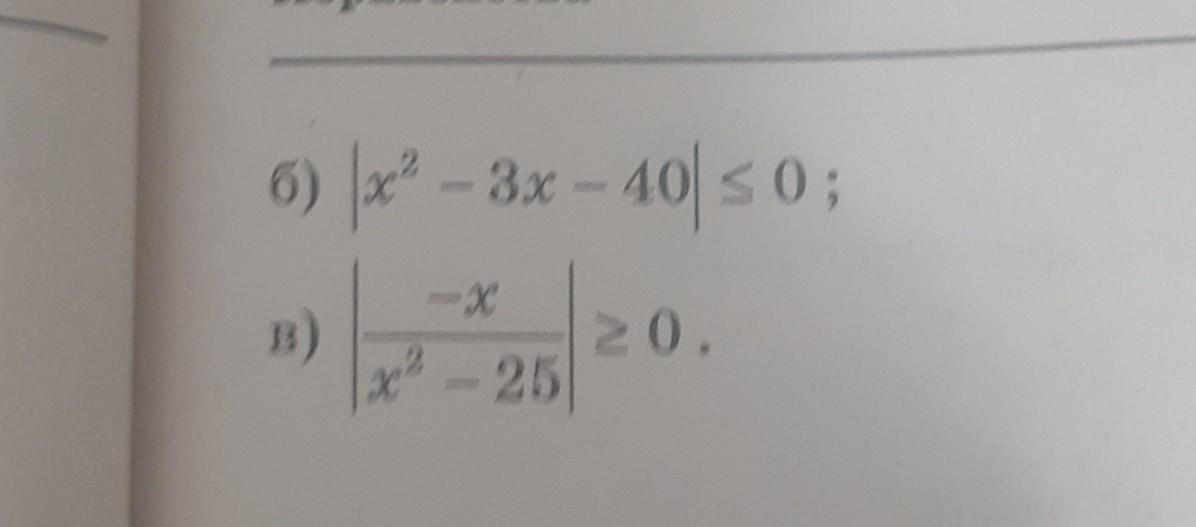Ответы
Ответ дал:
0
1) В первом случае понятно, что если левая часть под модулем то она ≥0 ,а значит ≤ выражение может быть только в точках где оно равно 0:
Значит решением неравенства будут x=-5, x=8.
2) Выражение под модулем всегда ≥0 , но есть условие на знаменатель выражения:
Значит решение неравенства
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад