Question

abc равнобедренный треугольник с основанием AC;CD -биссектриса угла C;угол ADC =150 градусов .Найдите угол B Срочно

Answer 1

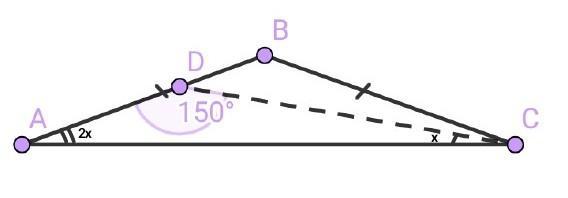
В равнобедренном треугольнике АВС с основанием АС провели биссектрису CD. Угол ADC = 150°. Найдите угол В.

Дано:

∆АВС — равнобедренный (АС — основание, АВ и ВС — боковые стороны).

CD — биссектриса <АСВ.

<ADC = 150°.

Найти:

<АВС = ?

Решение:

Так как CD — биссектриса <АСВ (по условию), то по определению биссектрисы —

<АСD = <DCB.

Пусть угол <ACD = x.

[В равнобедренном треугольнике углы при основании равны].

То есть —

<ВАС = <АСВ = 2*<ACD = 2x.

Рассмотрим ∆ADC.

По теореме о сумме углов треугольника —

<ADC+<DAC+<DCA = 180°

150°+2x+x = 180°

3x = 180°-150°

3х = 30°

х = 10°.

Тогда —

<ВАС = 2х = 2*10° = 20°.

Рассмотрим весь равнобедренный ∆АВС.

По выше сказанному —

<ВАС = <ВСА = 20°.

Тогда по теореме о сумме углов треугольника —

<АВС+<ВАС+<ВСА = 180°

<АВС+20°+20° = 180°

<АВС+40° = 180°

<АВС = 180°-40°

<АВС = 140°.

Ответ:

140°.