у прямокутному трикутнику медіана проведена із прямого кута дорівнює одному із катетів. знайти кут трикутника
Помогите срочно!!!
даю 25 баллов
Ответы
Ответ дал:
12
У прямоугольного треугольника медиана, проведённая из вершины прямого угла, равна одному из катетов. Найдите острые углы этого прямоугольного треугольника.
— — —
Дано:
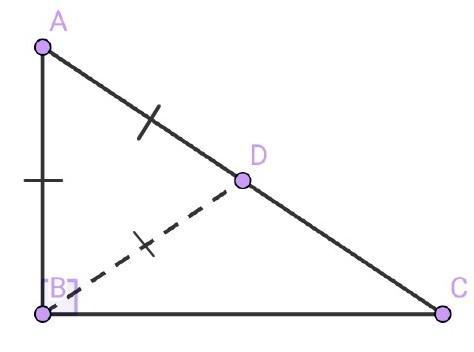
∆АВС — прямоугольный (<В = 90°).
BD — медиана, проведённая к гипотенузе.
АВ — катет.
АВ = BD.
Найти:
<А = ?
<С = ?
Решение:
Рассмотрим ∆BAD.
[В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна её половине].
То есть —
BD = AD.
Но также по условию —
BD = AB.
Следовательно —
BD = AB = AD.
Тогда ∆BAD — равносторонний (по определению).
[У равностороннего треугольника все углы равны по 60°].
То есть —
<А = <ADB = <ABD = 60°.
По теореме о сумме острых углов прямоугольного треугольника —
<С = 90°-<А
<С = 90°-60°
<С = 30°.
Ответ:
60°, 30°.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад