4^x-4^y=6, 4^(x+y)=16 система уравнений Решить нужно прошу пожалуйста есть пример ниже
Приложения:
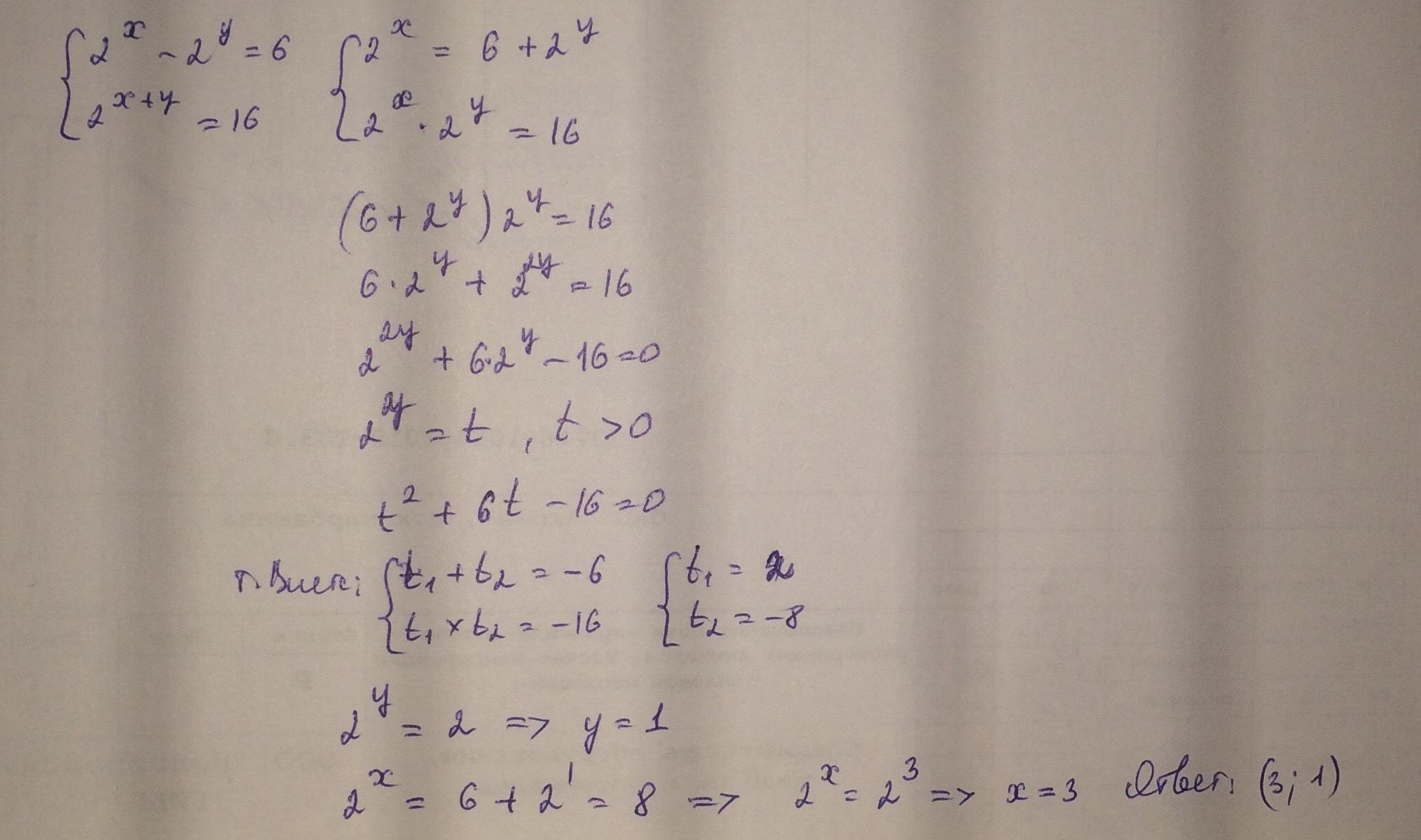
Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Умножаем все на
получаем
заменяем на новую переменную t, где t>0
получаем
решаем простейшее квадратное уравнение
получаем t={8;-2},
-2 выкидываем т.к t>0
далее без труда находим y
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад