Вычислить интегралы.
Приложения:
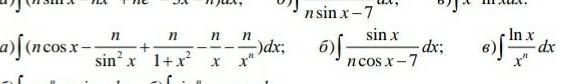
Аноним:
опять же. какое эн. т.е. номер варианта?
Так можно решить под предлогом "n", если нужно, Я могу потом сам подставить свою цифру.
т.е. эн - натуральное число. верно?
Да, Вы правы!
Ответы
Ответ дал:
2
а)∫(n*cosx-(n/(sin²x))+n/(1+x²)-(n/x)-(n/xⁿ))dx=
n*sinx-n(-ctgx)+n*arctgx-n*㏑IxI-n*(x¹⁻ⁿ/(1-n))+c=
n*sinx+n*ctgx+n*arctgx-n*㏑IxI-n*(x¹⁻ⁿ/(1-n))+c
б)∫(sinx/(ncosx-7))dx=-(1/n)∫d(ncosx-7)/(ncosx-7)=InI(n*cosx-7)I/n+c
в) ∫㏑хdx/xⁿ
интегрируем по частям u=㏑x⇒du=dx/x=x⁻¹dx
dv=dx/xⁿ⇒v=x¹ ⁻ⁿ/(1-n)
∫㏑хdx/xⁿ=(x¹ ⁻ⁿ/(1-n))*㏑x-∫(x¹ ⁻ⁿ/(1-n))*x⁻¹dx=(x¹ ⁻ⁿ/(1-n))*㏑x-∫(x⁻ⁿ/(-n+1))*dx=
(x¹ ⁻ⁿ/(1-n))*㏑x-(x¹⁻ⁿ/(1-n)²)*+c
Благодарю!
помогите мне, пожалуйста (несобственный интеграл)?
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад