Ответы
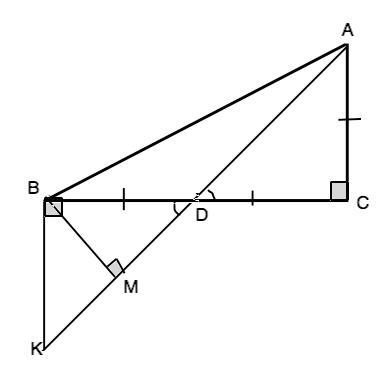
В прямоугольном (угол С=90°) треугольнике АСВ с вершины А опущена медиана АD. Если полученные отрезки АСCD, то найти тангенс угла между медианой и гипотенузой.
-------
Угол между медианой и гипотенузой - угол DAB.
АD - медиана => ВD=CD.
Если АС=СD, то прямоугольный ∆ АСD - равнобедренный.
Из вершины В проведем ВК║АС. Прямоугольные треугольники КВD=ACD по катету ( DB=CD - дано) и острому углу при D( вертикальны). => КD=AD
В ∆ КВD медиана ВМ (высота, биссектриса равнобедренного треугольника) делит КD пополам и перпендикулярна КD.. Медиана прямоугольного треугольника равна половине гипотенузы.
Примем ВМ=КМ=МD равным а. Тогда AD=KD=2a, АМ=3а.
Тангенс - отношение катета, противолежащего углу. к прилежащему катету. tg(MAB)=MB:MA=a:3a=1/3 - это ответ.
————
Ясно, что тот же результат получим, если будем находить длины отрезков через синус 45°.