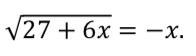Question

Решите уравнение: √27+6x=-x

Answer 1

$\sqrt{27+6x}=-x$

Найдем ОДЗ:

$27+6x\geq 0\\6x\geq -27\\x\geq -\frac{27}{6} \\x\geq -4\frac{3}{6}$

Возведем обе части уравнение в квадрат, при условии что обе части уравнения больше 0

По скольку в левой части есть арифметический корень, то левая часть больше 0.

-x>0

x<0

Решим уравнение:

$(\sqrt{27+6x})^{2} =(-x)^{2} \\27+6x=x^{2} \\x^{2} -6x-27=0\\D=36+108=144=12^{2} \\x1=\frac{6+12}{2} =\frac{18}{2} =9\\x2=\frac{6-12}{2} =\frac{-6}{2} =-3$

9 нам не подходит, поскольку оно больше 0, а -3 меньше нуля и больше -27/6, поэтому -3 нам подходит.

Ответ: -3

Answer 2

Ответ: х=-3.

Объяснение: