Предмет: Математика
Автор: SnakeCheat
Вопрос задан 3 года назад

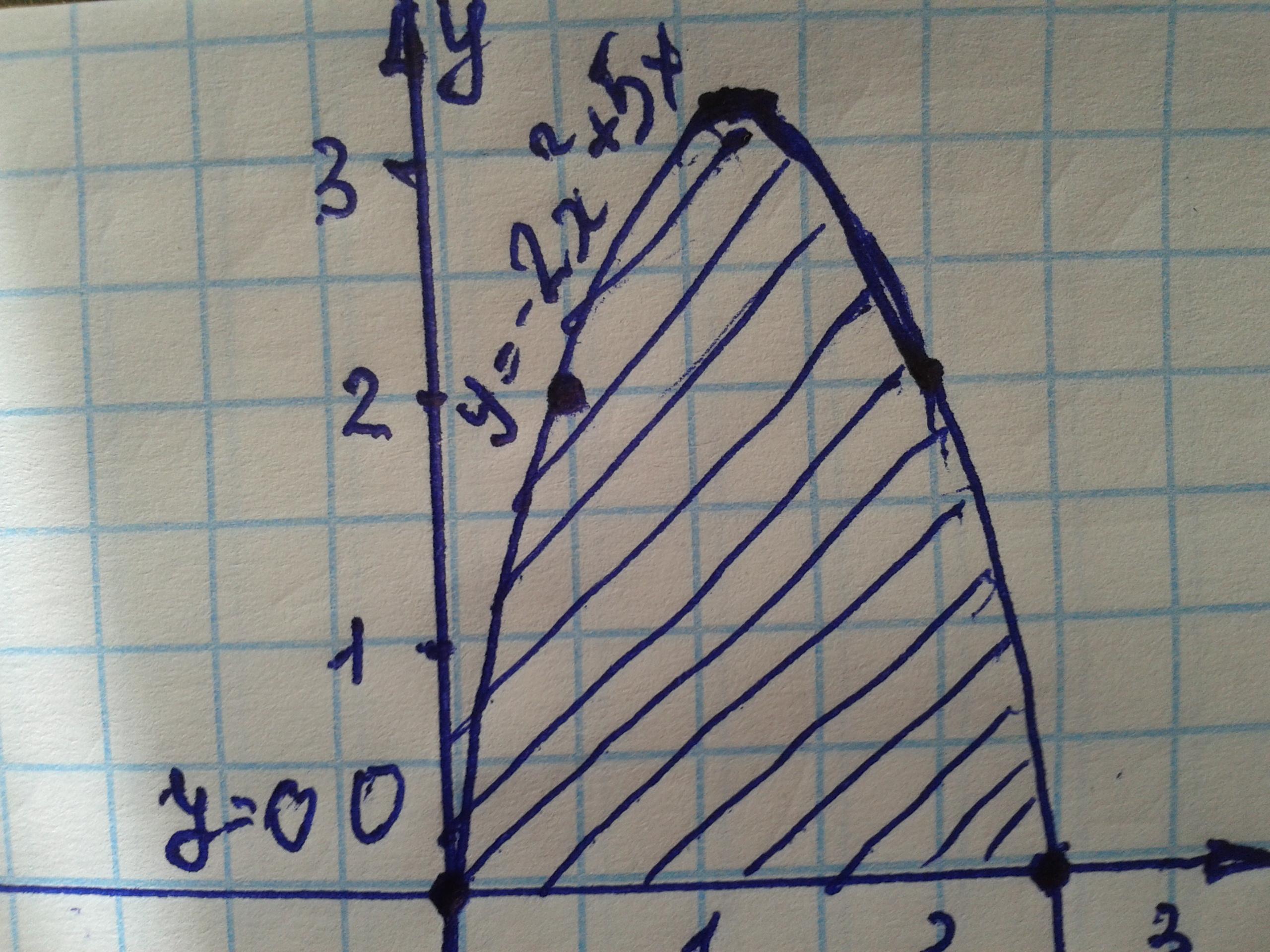
Найдите площадь фигуры, ограниченной линиями: у=-2x^2+5x,y=0.
Если не увидите ответа, то знайте, я уже отчислен(

orjabinina: что непонятно 1) как параболу построить? 2) как площадь искать? 3) как штриховать на чертеже? 4) как применять формулу Ньютона-Лейбница ????

SnakeCheat: всё)

orjabinina: чертеж сделал ? Если -нет , то сделай.

SnakeCheat: понимаете? я математику совсем забыл, теперь вообще не понимаю как чертить или что чертить

orjabinina: S= ∫ ( -2x²+5х))dx=-2/3*x³+5/2*x² =( по формуле Ньютона-Лейбница )= -2/3*( 5/2)³+5/2*(5/2)² )-( -2/3*0³+5/2*0² )=-2/3*125/8+5/2*25/4-0=

orjabinina: =125/8(-2/3+1)=125/8*1/3=125/24.

orjabinina: Чертеж начертить не могу. Сообрази сам.1) на оси ох отметь 0 и 2,5.затем через эти точки проведи параболу ветвни вниз ( не знаешь как посмотри в инете). Внутри параболы будет область =это криволинейная трапеция. Ее надо заштриховать.

orjabinina: Может кто-нибудь тебе кинет ответ. Жди.

SnakeCheat: спасибо) пойду вешаться)

orjabinina: эй, ты живой?

Ответы

Ответ дал: sangers1959

$y=-2x^2+5x, y=0;S=?\\-2x^2+5x=0|:(-1)\\2x^2-5x=0\\x*(2x-5)=0\\x_1=0\\2x-5=0\\3x=5|:2\\x=2,5.\\S=\int\limits^{2,5}_0 {(-2x^2+5x-0)} \, dx =\int\limits^{2,5}_0 {(5x-2x^2)} \, dx =(\frac{5x^2}{2}-\frac{2x^3}{3})|_0^{2,5}=\\ =\frac{5*2,5^2}{2} -\frac{2*2,5^3}{3}-(\frac{5*0^2}{2}-\frac{2*0^3}{3})=2,5*2,5^2-\frac{2}{3} *2,5^3=2,5^3-\frac{2}{3}*2,5^3=\frac{1}{3}*(2\frac{1}{2}) ^3=\frac{1}{3}*(\frac{5}{2})^3= \frac{1}{3}*\frac{125}{8}=\frac{125}{24}=5\frac{5}{24} .$