Ответы
Ответ дал:
1
Ответ:
Приложения:

Jackoe89:
Благодарю. А какую программу вы испольуете, для использования мат. символики?
LaTex
Ответ дал:
0
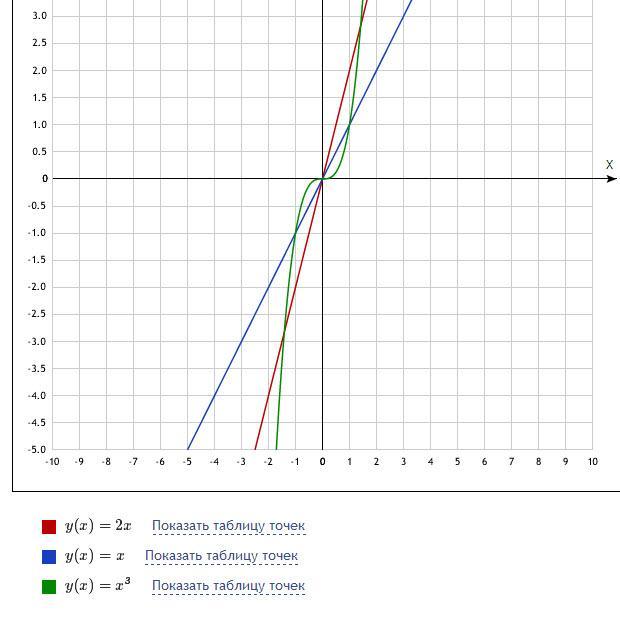
Объяснение: смотрите график и решение во вложении
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад