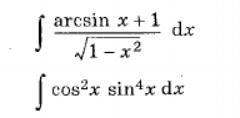Question

Найти неопределённый интеграл

Answer 1

1. ∫(arcsinx+1)dx/(√1-x²)=∫(arcsinx)dx/(√1-x²)+∫dx/(√1-x²)=

∫(arcsinx)*d(arcsinx)+∫dx/(√1-x²)=(arcsinx)²/2+(arcsinx)+c

2. ∫cos²x*sin⁴xdx=(1/8)∫(1+cos2x)(1-cos2x)²dx=(1/8)∫(1-cos²2x)(1-cos2x)dx=

(1/8)∫(1-cos²2x-cos2x+cos³2x)dx=

(1/8)∫(1-(1+cos4x)/2-cos2x+(1+cos4x)/2*cos2x)dx=

(1/8)∫(1-cos2x-(1+cos4x)/2+((1+cos4x)/2)*cos2x)dx=

(1/8)∫(1-cos2x-1/2-((cos4x)/2)+((1/2)cos2x+(1/2)*cos2x*cos4x)dx=

(1/8)∫(1-cos2x-1/2-((cos4x)/2)+((1/2)cos2x+(1/2)*cos2x*cos4x)dx=

(1/8)∫(1-cos2x-1/2-((cos4x)/2)+((1/2)cos2x+(1/4)*cos2x+(1/4)cos6x)dx=

(1/8)∫(1/2-(1/4)cos2x-((cos4x)/2)+(1/4)cos6x)dx=

(1/16)*∫(1-(1/2)cos2x-cos4x+(1/2)cos6x)dx=

(х/16)-(sin2x/64)-(sin4x/64)+(sin6x/192)+c

Answer 2

Ответ:

$1)\ \ \int \dfrac{arcsinx+1}{\sqrt{1-x^2}}\, dx=\int arcsinx\cdot \dfrac{dx}{\sqrt{1-x^2}}+\int \dfrac{dx}{\sqrt{1-x^2}}=\\\\\\=\int arcsinx\cdot d(arcsinx)+\int d(arcsinx)=\dfrac{1}{2}\cdot arcsin^2x+arcsinx+C$

$2)\ \ \int cos^2x\cdot sin^4x\, dx=\int (sinx\cdot cosx)^2\cdot sin^2x\, dx=\\\\\\=\int \Big(\dfrac{1}{2}\, sin2x\Big)^2\cdot \dfrac{1-cos2x}{2}\, dx=\dfrac{1}{8}\int sin^22x\cdot (1-cos2x)\, dx=\\\\\\=\dfrac{1}{8}\int sin^22x\, dx-\dfrac{1}{8}\int sin^22x\cdot cos2x\, dx=\dfrac{1}{8}\int \dfrac{1-cos4x}{2}\, dx-\\\\\\-\dfrac{1}{8}\cdot \dfrac{1}{2} \int sin^22x\cdot d(sin2x)=\dfrac{1}{16}\cdot (x-\dfrac{1}{4}\, sin4x)-\dfrac{1}{16}\cdot \dfrac{sin^32x}{3}+C$