Как схематически набросить график x^2/25-y^2/16=1 Там нужны асимптоты в основном И в центре еще вроде какой-то прямоугольник получается (но это не точно)
orjabinina:
Две симметричные относительно оу параболы (забыла их верное название). С центрами в (5 0 ) и (-5 0 )
Прижатые к оси их
Ответы
Ответ дал:
3
Это гипербола с большей полуосью и меньшей полуосью
.
Асимптоты гиперболы:
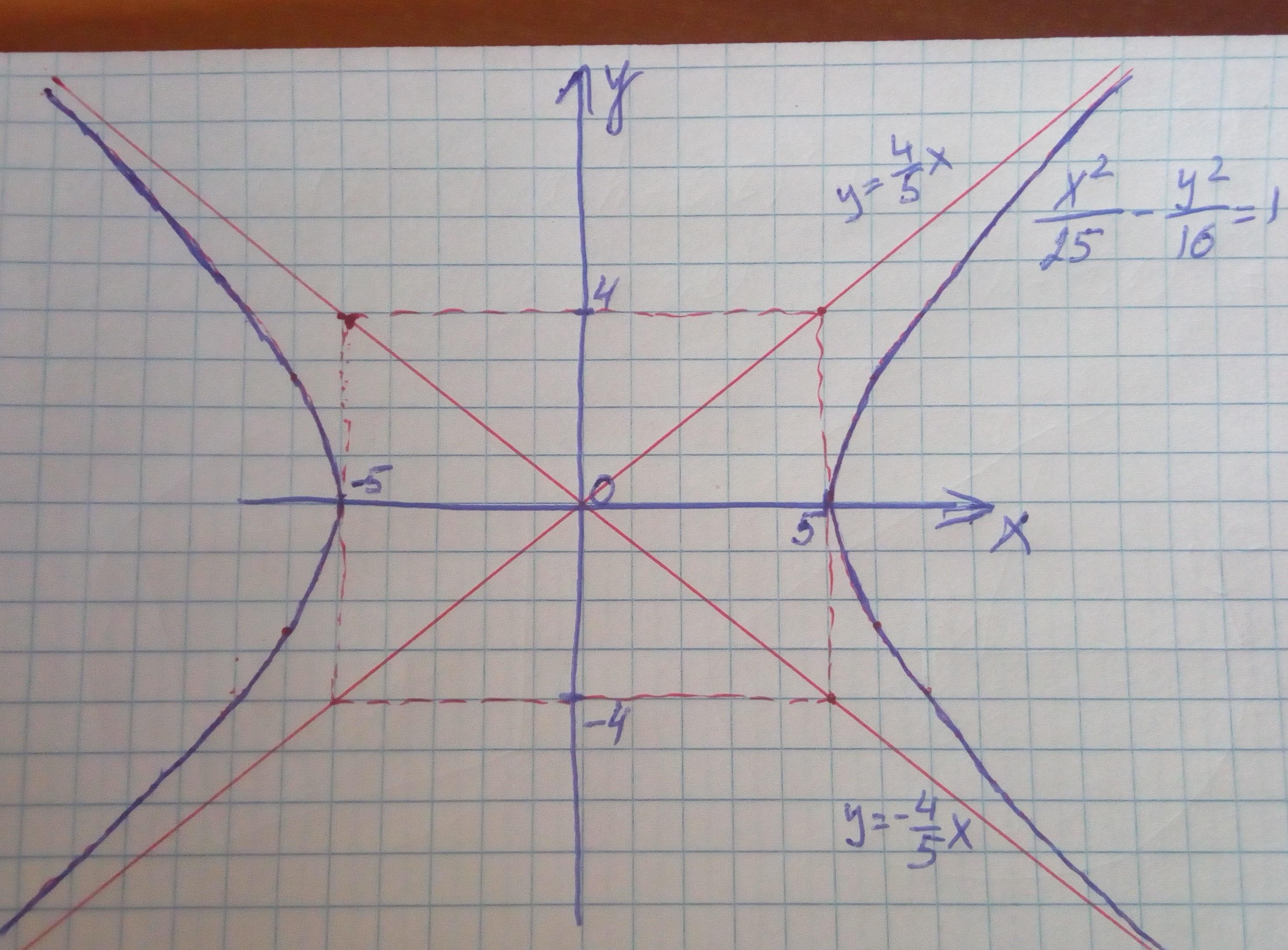
Изобразить асимптоты и график может помочь прямоугольник размера со сторонами, параллельными осям координат, проходящий через точки
. Асимптоты проходят через противоположные вершины прямоугольника.
Сам график касается этого прямоугольника в точках , то есть в точках
. Далее график приближается к асимптотам. Для более точного построения можно просчитать пару точек.
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад