Question

В остроугольном треугольнике ABC проведена высота BH. Из точки H на стороны AB и BC опустили перпендикуляры HL и HK соответственно. BH=a, $\dfrac{S_{LBK}}{S_{ABC}} =\dfrac1{n^2}$ .
1. Доказать, что треугольники LBK и ABCподобны.
2. Найти радиус окружности, описанной около треугольника ABC.

Answer 1

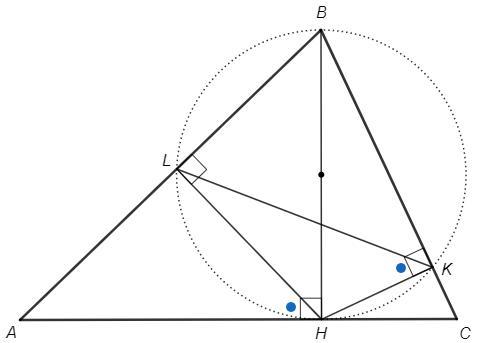
BLHK - вписанный четырехугольник (т.к. противоположные углы прямые)

Прямой угол опирается на диаметр BH, AC - касательная (т.к. AC⊥BH)

LHA =LH/2 (угол между касательной и хордой) =LKH

A =90-LHA =90-LKH =BKL

△ABC~△KBL (по двум углам)

S(ABC)/S(KBL) =k^2 => k=n

R_KBL =BH/2 =a/2

R_ABC/R_KBL =k =n => R_ABC =na/2