Решите пожалуйста 30 баллов
Приложения:
Iife20:
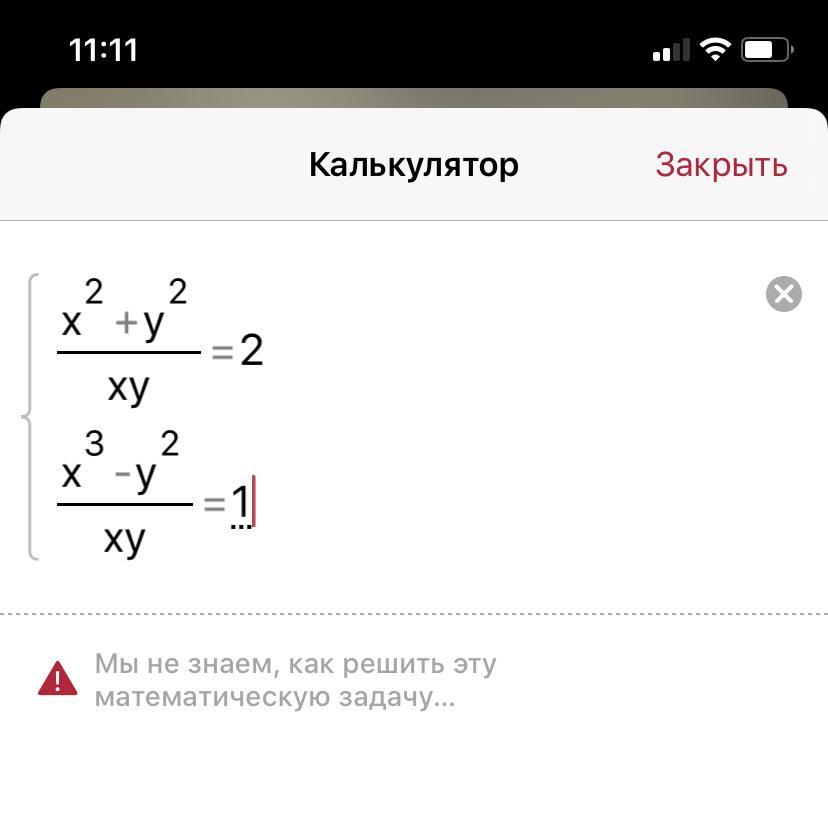
Это система уравнений?
С первого уравнения х^2-2ху+у^2=0, х=у. Подставить во второе и получаем ответ х=2, у=2.
Ответы
Ответ дал:
0
Ответ дал:
0
Ответ:
Объяснение:
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад