Ответы
Ответ дал:
3
Формулы:
а³–b³= (a–b)(a²+ab+b²).
a²–b²= (a–b)(a+b).
(a+b)²= a²+2ab+b².
Приложения:
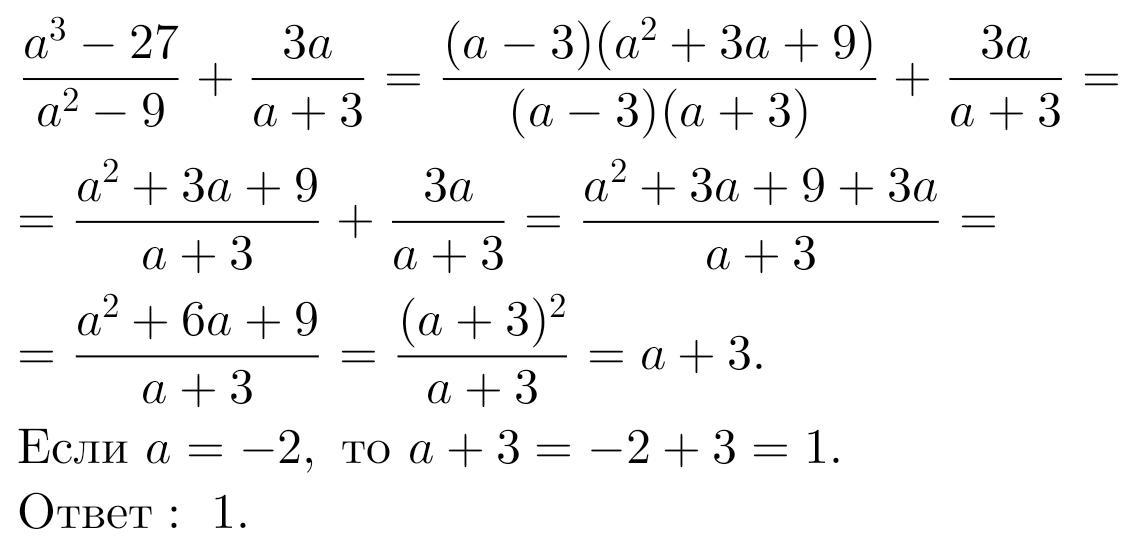
Kierra:
(а–1) в числителе и в знаменателе сокращаются, остаётся (2а+1)/(а+1)
Не смогла разобраться как получилось а(2а+1)–(2а+1)=(2а+1)(а–1). То есть, как убрали а и минус. Не подскажете?
Разложите на множители. Представьте, (2а+1) — это отдельный множитель. Пусть 2а+1=х. Тогда а(2а+1)–(2а+1)=2х–х. "х" вынесите за скобки.
2х–х= х(а–1). Помним, что такое х? Отсюда и получается
а(2а+1)–(2а+1)=(2а+1)(а–1). Повторите тему:)
2х–х= х(а–1). Помним, что такое х? Отсюда и получается
а(2а+1)–(2а+1)=(2а+1)(а–1). Повторите тему:)
Там ах–х. Не 2а!
Случайно)
а(2а+1)–(2а+1)= а•(2а+1)–1•(2а+1)= (2а+1)(а-1)....
Плохо, если этого не помните. Это начало всей алгебры...
Я школу очень давно закончила. Сейчас просто пытаюсь освежить память для экзамена. Спасибо Вам большое, что потратили время и помогли разобраться)
Удачи Вам на экзамене!!))
Благодарю :)
Вас заинтересует
2 года назад
2 года назад