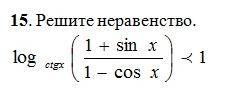Question

Решите неравенство............

Answer 1

Применяя метод рационализации получаем систему:

{ctgx >0⇒ x∈ (πm; (π/2)+πm), m∈Z

{(1+sinx)/(1-cosx) >0⇒  x≠(-π/2)+2πk, x≠2πn, k, n ∈Z

{(ctgx-1)·((1+sinx)/(1-cosx)  - ctgx ) <0

Решаем третье неравенство системы:

$(\frac{cosx}{sinx}-1)\cdot (\frac{1+sinx}{1-cosx} - \frac{cosx}{sinx})<0\\\\\frac{cosx-sinx}{sinx}\cdot \frac{(1+sinx)sinx-cosx(1-cosx)}{(1-cosx)sinx} <0\\\\ \frac{(cosx-sinx)(sinx-cosx+1)}{(1-cosx)sin^2x} <0$

Решаем методом интервалов.

Находим нули числителя:

$cosx-sinx=0$    или        $sinx-cosx+1=0$    вводим вспомог. угол

$tgx=1$                   или      $\frac{1}{\sqrt{2}} cosx-\frac{1}{\sqrt{2}}sinx=\frac{1}{\sqrt{2}}$

$x=\frac{\pi }{4} +\pi t, t\in Z$   или     $x+\frac{\pi }{4}=\pm\frac{\pi }{4}+2 \pi s, s\in Z$  не входят в ОДЗ

Находим нули знаменателя:

$1-cosx=0$         или    $sinx=0$

$x=2\pi n, n\in Z$    или  $x=\pi k, k \in Z$

(0) __+__ (π/4)___-__ (π/2)

При х=π/6

$\frac{(cos\frac{\pi }{6} -sin\frac{\pi }{6})(sin\frac{\pi }{6}-cos\frac{\pi }{6}+1)}{(1-cos\frac{\pi }{6})sin^2\frac{\pi }{6}} >0$

При х=π/3

$\frac{(cos\frac{\pi }{3} -sin\frac{\pi }{3})(sin\frac{\pi }{3}-cos\frac{\pi }{3}+1)}{(1-cos\frac{\pi }{3})sin^2\frac{\pi }{3}} <0$

О т в е т.( (π/4)+πn; (π/2)+πn), n∈Z