Как вычислить степень с рациональным показателем? Напишите правильный подробный порядок вычисления. Ответ - 0.5 . Мне нужно узнать как это решать.
Приложения:
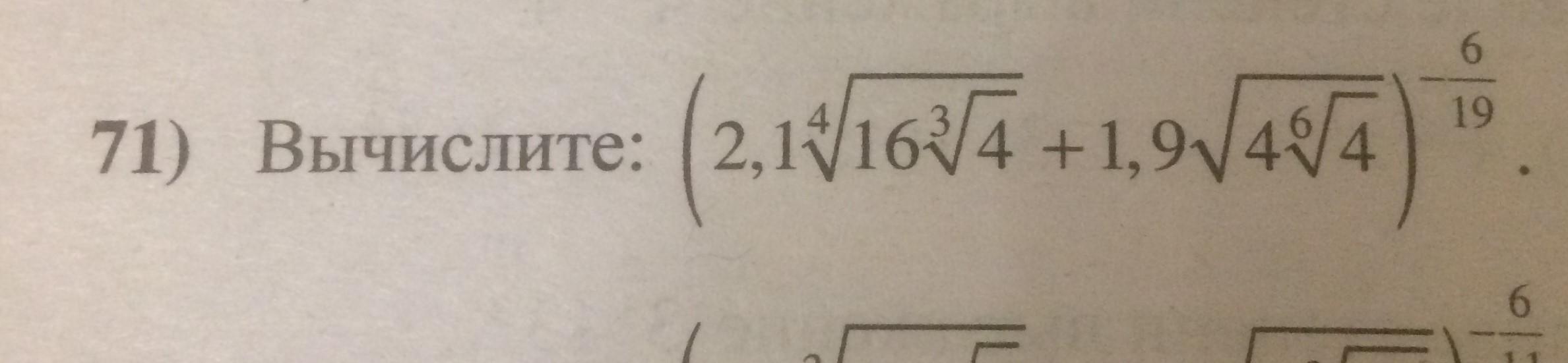
Ответы
Ответ дал:
1
Ответ:
1/2
Пошаговое объяснение:
n√(a^m) = a^(m/n)
16∛4 = 4^2 * 4^(1/3) = 4^(2 + 1/3) = 4^(7/3)
(4^(7/3))^(1/4) = 4^(7*1/(3*4)) = 4^(7/12)
4*4^(1/6) = 4^(1 + 1/6) = 4^(7/6)
(4^(7/6))^(1/2) = 4^(7/12)
(4^(7/12) * (2,1 + 1,9))^(-6/19) = (4^(7/12) * 4)^(-6/19) = (4^(7/12 + 1))^(-6/19) = (4^(19/12))^(-6/19) = 4^(19*(-6)/(12*19) = 4^(-1/2) = 1/(4^(1/2)) = 1/√4 = 1/2
raptorvideo:
Извините , а вы можете это написать на листке чтобы было более понятно?
у меня нет возможности кинуть скан
Эх , как вы все это в голове держите... Просто вырвали целые куски и переставили . Это уже автоматизм , да? Никакие правила не помогут.
Нет, не опускайте руки, введите в поисковике свойства степеней, просмотрите и запомните. Неважно какая степень, правила одни и те же. С рацухами нужно знать только специфику, что n√(a^m) = a^(m/n) и все.
Ну , я и говорю что знание правил не поможет решить все это дело . Все эти правила я специально смотрел и у меня ничего не получалось , а здесь оказывается нужно оторвать 2.1 и 1.9 + корни 4 степени , это уже автоматизм.
Я просто вынес общий множитель 4^(7/12) и никто Вам не запрещает делать по действиям, в этом нет ничего зазорного
Я дико извиняюсь , но куда делать семерка - (4^(7/12 + 1))^(-6/19) = (4^(19/12))^(-6/19) ? :D
7/12 + 1 = 7/12 + 12/12 = (7 + 12)/12 = 19/12
Вы по каким учебникам учились?))
Мордкович в 2-х частях 7- 11 классы. 1-я часть - красный учебник (только теория с разобранными примерами). 2-я часть - синий (задачник, отработка теории)
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад