Ответы
Ответ дал:
4
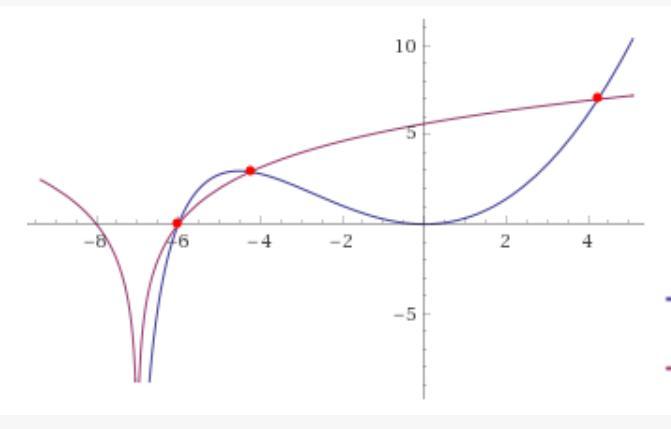
Дано неравенство x² * log(512,(x+7))<= log(2,(x² + 14x + 49)).
Учтём, что 512 = 2^9 и x² + 14x + 49 = (x + 7)² .
Тогда исходное неравенство примет вид:
(x²log(2, (x + 7))/9) ≤ 2log(2, (x + 7)).
Отсюда делаем вывод: логарифм нуля не существует, х ≠ -7.
Далее, логарифм 1 при любом основании равен 0.
Значит, это один из корней неравенства.
Если логарифм не равен 0, то тна него можно сократить
Получим х² = 18, х = ±√18 = ±3√2.
Ответ: -7 < x ≤ -6, -3√2 ≤ x ≤ 3√2.
Приложения:
Ответ дал:
2
Решение приложено
--------------------------------------------------------------------------------------------
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
9 лет назад