дан правильный тетраэдр с ребром √2 найдите расстояние между противоположными ребрами
orjabinina:
ответ есть?
не очень"красивый"получился √ (7/2)
ошиблась в арифметике.
Ответы
Ответ дал:
1
В правильном тетраэдре все грани равносторонни треугольники.
В равностороннем треугольнике со стороной a
высота, медиана равна (a√3/2)
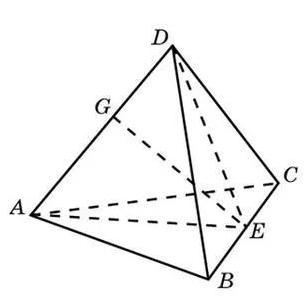
Пусть E- середина ВС.
G - середина AD.
EG- медиана равнобедренного треугольника ADE⇒EG⊥AD
EG- медиана равнобедренного треугольника BGC⇒EG⊥BC
EG - перпендикуляр к ребрам AD и BC.
Это и есть кратчайшее расстояние между ребрами
По теореме Пифагора из Δ AGE:
EG²=AF²-AG²=(a√3/2)²-(a/2)²=(3a²/4)-(a²/4)=2a²/4
EG=(a√2)/2
В задаче a=√2
d=EG=(√2·√2)/2=1
О т в е т. 1
Приложения:
Вас заинтересует
2 года назад
2 года назад
2 года назад
9 лет назад
9 лет назад