т29) Если sinB+ cosB= 1,35 , то какой четверти координатной плоскости принадлежит точка, совпадающая с углом B ?
Помогите пожалуйста!
Спасибо!
Ответы
Ответ дал:
2
Ответ:
в=приблизительно 27-28°
угол первой четверти.
Приложения:
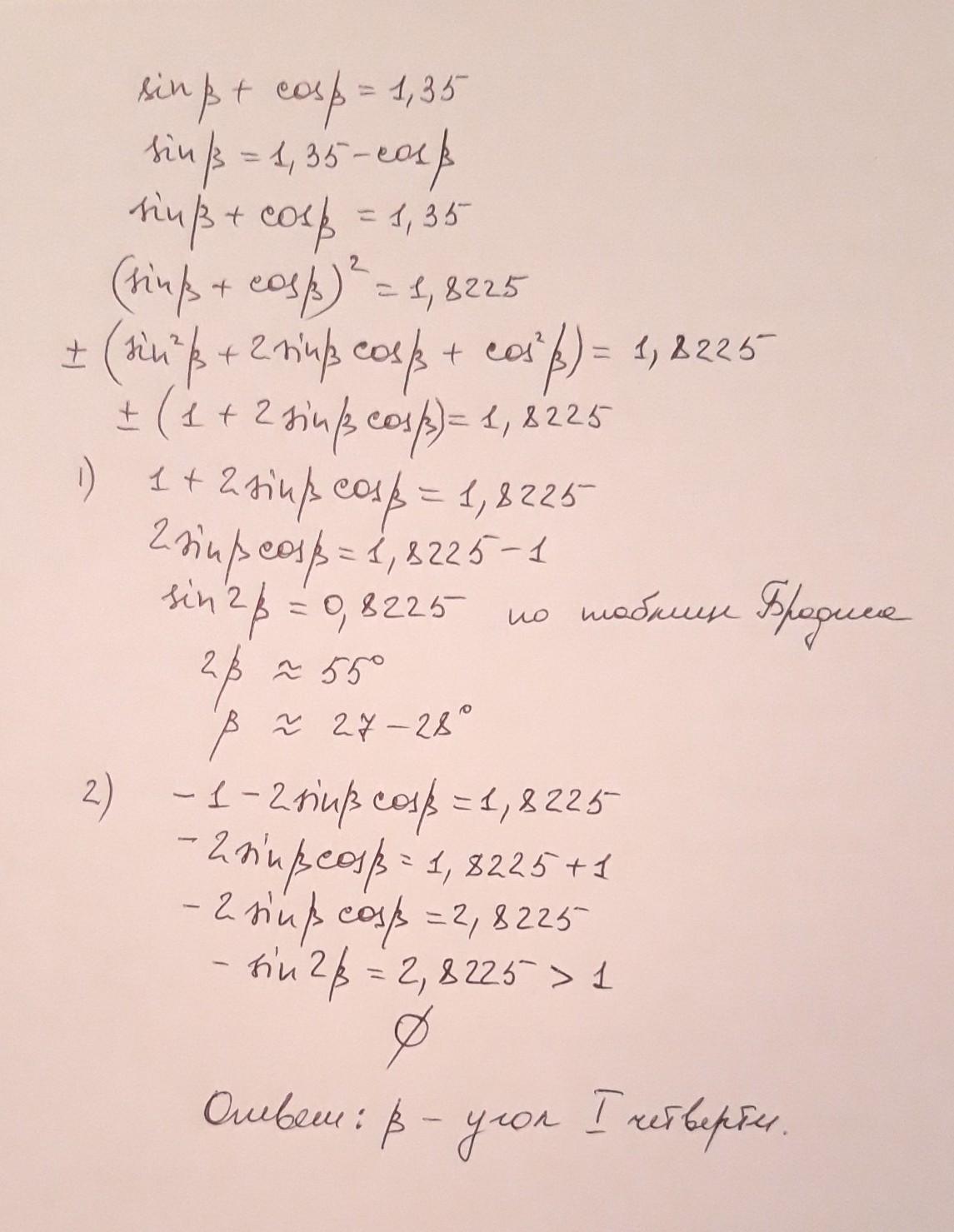
gnomiha211:
спасибо большое))
Ответ дал:
4
Можно воспользоваться формулой, связывающей синус и косинус одного угла.
.
Отсюда sin(a + (pi/4)) = 1,35/√2 = 0,954594.
(a + (pi/4)) = arcsin(0,954594) = 72,668°.
a = 72,668 - 45 = 27,668°.
Ответ: точка, совпадающая с углом B, принадлежит 1 четверти.
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад