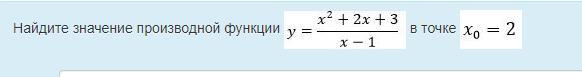Ответы
Ответ дал:
3
Ответ:
-5
Пошаговое объяснение:
Исходная функция представляет собой отношение двух функций. Производная отношения находится по следующему правилу
Применяя это правило к данной функции, получим
Значение производной в указанной точке
.
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад