задача про трапецию, ответ отмечен, мне нужно решение
Приложения:
Iife20:
что такое va?
там опечатка, это и
спасибо
Ответы
Ответ дал:
2
Отношение оснований BC и AD трапеции ABCD равно 1 : 5. Точка Е и K находятся на стороне CD и делят ее в отношене 1:2:1. Точка F делит сторону АВ пополам. Найдите отношение площади трапеции на площадь треугольника EFK.
Решение:
Проведём среднюю линию . Средняя линия трапеции делит её высоту пополам и обозначим
,
Пусть тогда, E — середина отрезка CG и точка G — середина отрезка EK (т.к. EG = GK = 2x - x = x). Следовательно,
Обозначим
Определим отношение площадей трапеций ABCD и FBCG
(1)
Определим отношение площадей трапеции FBCG и треугольника FEG
Поскольку G — середина EK, то FG — медиана треугольника FEK и делит она площадь треугольника пополам.
Выразив отсюда и подставив в равенство (1), мы получим
Ответ: 4 : 1.
Приложения:
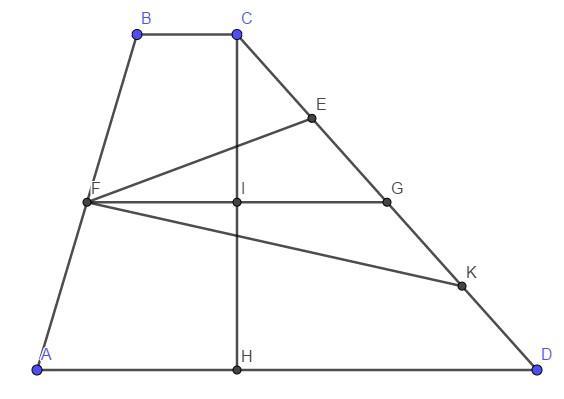
Премного благодарна! Такую тяжелую для меня задачу так легко объяснили! Только у меня один вопрос есть, где площадь треугольника FEG мы взяли половину произведения стороны FG и 1/4 высоты трапеции, значит если есть какой-то отрезок, перпендикулярный стороне треугольника, мы можем применить его в качестве высоты, опущенной на сторону треугольника?
проведите на среднюю линию EG, но так как Е - середина, то перпендикуляр опущенный EG является средней линией треугольника CIG
Обозначьте EH эту высоту. получится что EH = CI/2 = (h/2)/2 = h/4
Спасибо большое
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
9 лет назад