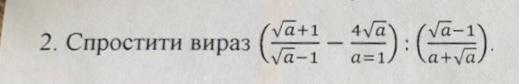Ответы
Ответ дал:
0
Ответ:√а
Объяснение:1) (√а+1)/(√а-1)-(4√а/(а-1))=(а+1-4√а+2√а)/(а-1)=(√а-1)²/(а-1)
=(√а-1)/(√а+1)
2) ((√а-1)/(√а+1)):((√а-1)/(√а*(√а+1))=
(√а*(√а+1)*(√а-1))/((√а+1)*(√а-1))=√а
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад