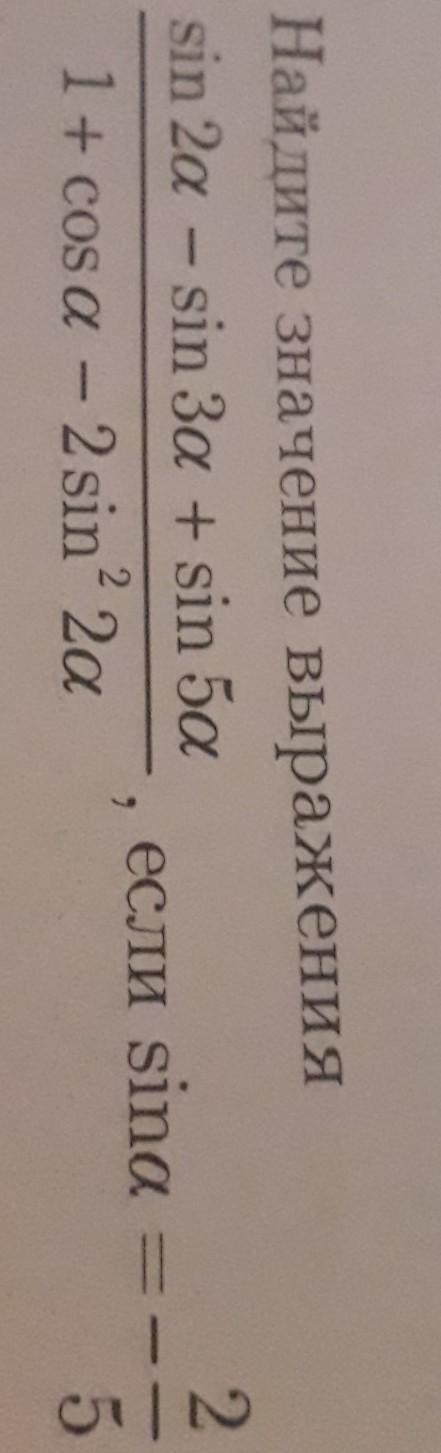Ответы
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Преобразуем числитель по формуле разности синусов:
Числитель примет вид: sin2α+2sinαcos4α=2sinαcosα+2sinαcos4α=2sinα(cosα+cos4α)
Преобразуем знаменатель по формуле двойного косинуса
1-2sin²2α=cos²2α-sin²2α=cos4α.
Теперь знаменатель примет вид: cosα+cos4α.
Запишем преобразованную дробь:
.
Подставим известные данные:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад