Помогите решить!! Более подробно нужно!! 100б
Приложения:
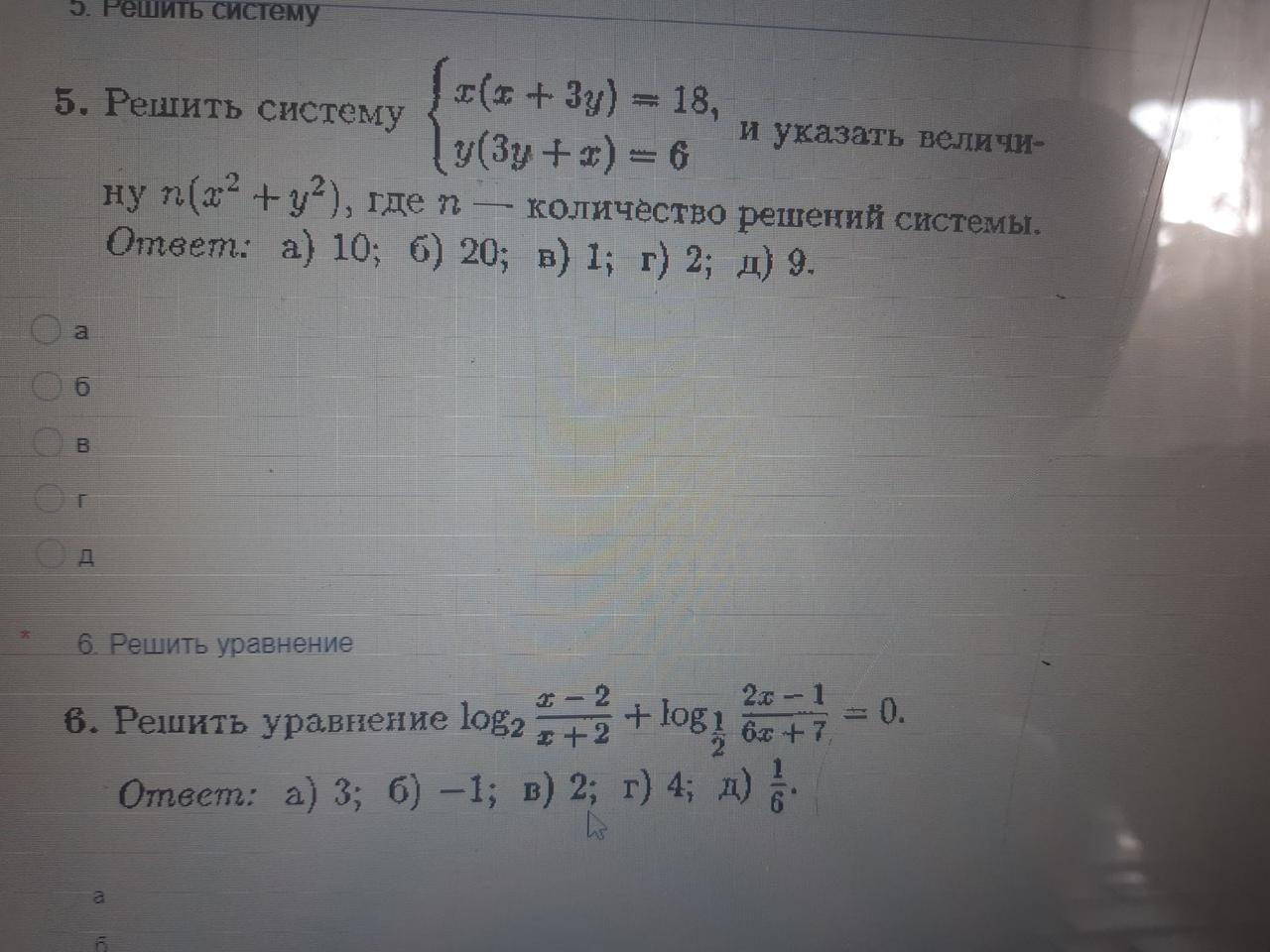
Аноним:
тебе 5 или 6
желательно оба номера!
Ответы
Ответ дал:
1
Ответ:
Объяснение:
////////////////
Приложения:


5 какой ответ?
б. обведено же
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад