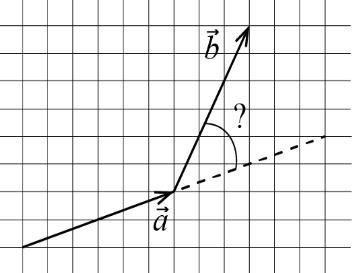
Определите угол между векторами
Приложения:
ВикаБач:
a={6;2}. b={3;6}. ab=6*3+2*6=30. |a|=sqrt(36+4)=2*sqrt(10). |b|=sqrt(9+36)=3*sqrt(5). CosA=30/(6*sqrt(50))=5/5sqrt(2)=1/sqrt(2). A=45градусов.
Ответы
Ответ дал:
1
Ответ:α=45°
Объяснение: По рисунку видны координаты векторов при условии, что начало системы координат является точкой пересечения этих векторов. тогда a(6;2); b(3;6)
Найдем косинус угла между векторами, поделив их скалярное произведение на произведение длин этих векторов.
а*в=6*3+2*6=30
IaI=√(6²+2²)=√40=2√10;
IbI=√(3²+6²)=√45=3√5;
cosα=30/(2√10*3√5)=30/(6*5*√2)=1/√2;
α=45°
Вас заинтересует
2 года назад
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад