Помогите решить срочно даю 30 баллов
Приложения:
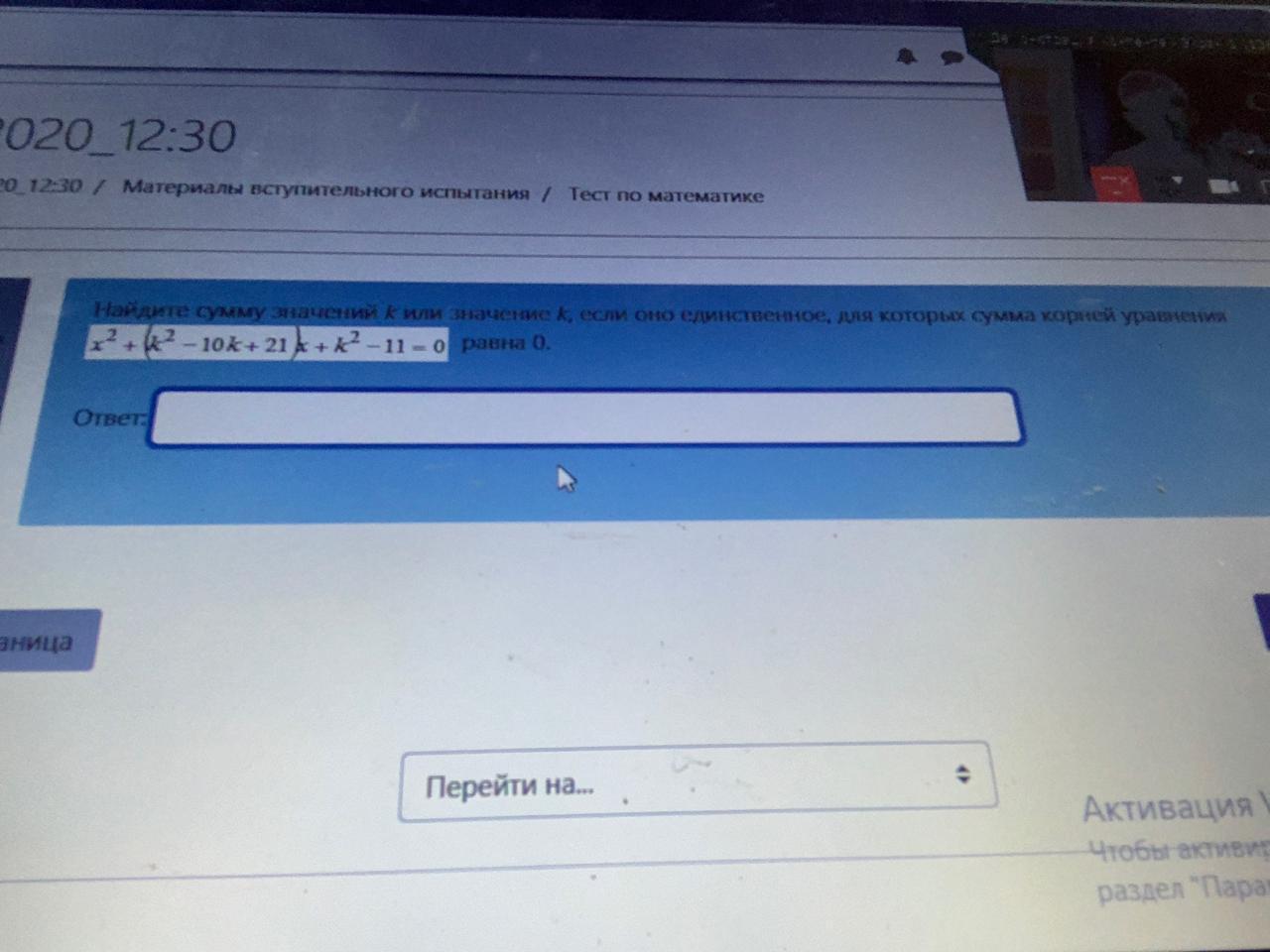
Kierra:
Сумма корней данного кв.уравнения равна нулю, если –(k²–10k+21)=0. => k=3 или k=7. 7 не подходит, т.к. в таком случае уравнение не будет иметь решений. Остаётся 3. Ответ k=3.
Ответы
Ответ дал:
0
Ответ:
Пошаговое объяснение:
x1+x2=-(k²-10k+21)
k²-10k+21=0
D=100-84=16
k1= (10-4)/2= 3
k2= (10+4)/2=7 - не корень, при k=7, x ∉R
ответ 3
Ответ дал:
0
х²+(к²-10к+21)х+к²-11=0
сумма корней равна нулю, если по Виету
-(к²-10к+21)=0⇒По Виету к=7, к=3.
Кроме того, произведение корней должно равняться свободному члену с тем же знаком, т.е. к²-11. если к=7, то
к=7; 49-11=38
Уравнение х²+38=0, ∅
к=3; 9-11=-2
х²-2=0, здесь х=±√2, их сумма равна нулю.
Ответ к=3
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад