т38) Решите уравнение tg(2x+3)= tg(3x-2)
Буду благодарна, если распишете поподробнее, ибо хочу понять метод решения подобных уравнений( в моих вопросах есть еще похожие).
Заранее большое спасибо!!
Приложения:
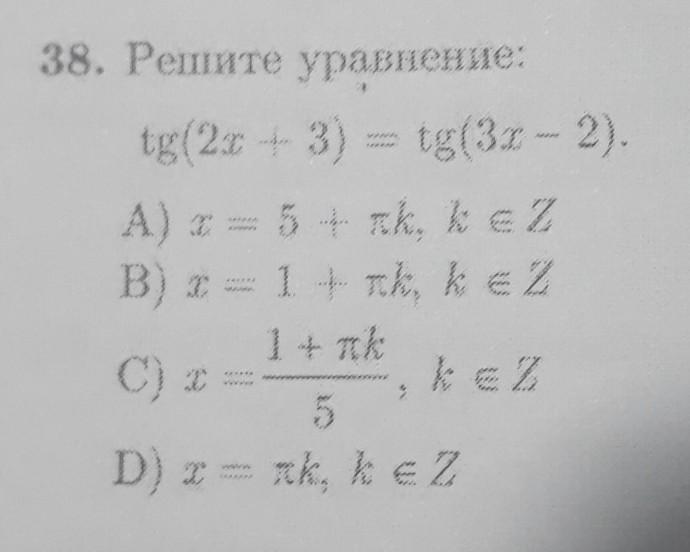
Ответы
Ответ дал:
1
Ответ:
gnomiha211:
Спасибо еще раз) Вы очень помогли!
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад