Помогите пожалуйста. Очень срочно! Даю 30 баллов
Приложения:
orjabinina:
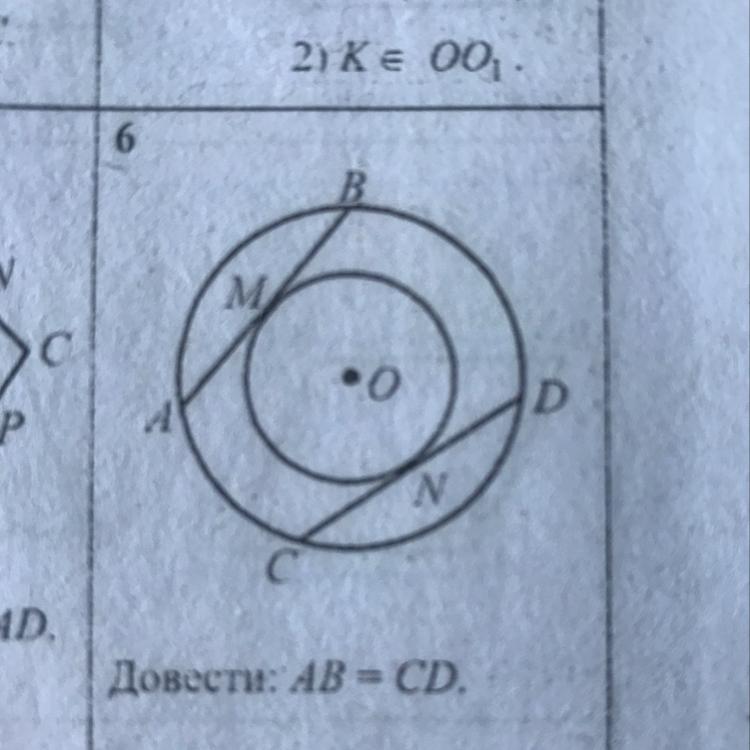
Δ АОМ=Δ СОД
Извините, а можно полное объяснение)
ΔОВМ=ΔОСN как прямоугольные ( радиусы ОМ и ОN проведены в точку касания) по гипотенузе ( ВО=ОС) и катету (ОМ= ОN ). В равных треугольниках соответственные элементы равны , значит
Спасибо)
∠ МВО=∠ NCO. Рассмотрим
ΔАВО и ΔДСО они равнобедренные , т.к. ОВ=ОА= Ос=ОД=R внешней окружности.
Выше можно не читать. есть доказательство короче . Решение 1) ΔОВМ=ΔОСN как прямоугольные ( радиусы ОМ и ОN проведены в точку касания) по гипотенузе ( ВО=ОС) и катету (ОМ= ОN ). В равных треугольниках соответственные элементы равны , значит ВМ=CN. 2) ΔОМА=ΔОДN аналогично. Значит АМ=ND. Получили АМ+МВ=CN+ND , значит АВ=СД
Понятно?
Да, огромное спасибо
Ответы
Ответ дал:
2
Ответ:
======================================
Объяснение:
Приложения:

Вас заинтересует
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад