Ответы
Ответ дал:
5
Ответ:
Объяснение: в приложении
Также можно было изначально заметить, что, если перенести все слагаемые в левую часть, у получившегося многочлена сумма коэффициентов при чётных степенях совпадает с суммой коэффициентов при нечётных степенях, а значит многочлен делится на (x+1), и тогда можно бы было поделить его на (x+1). (Фото 2)
Приложения:
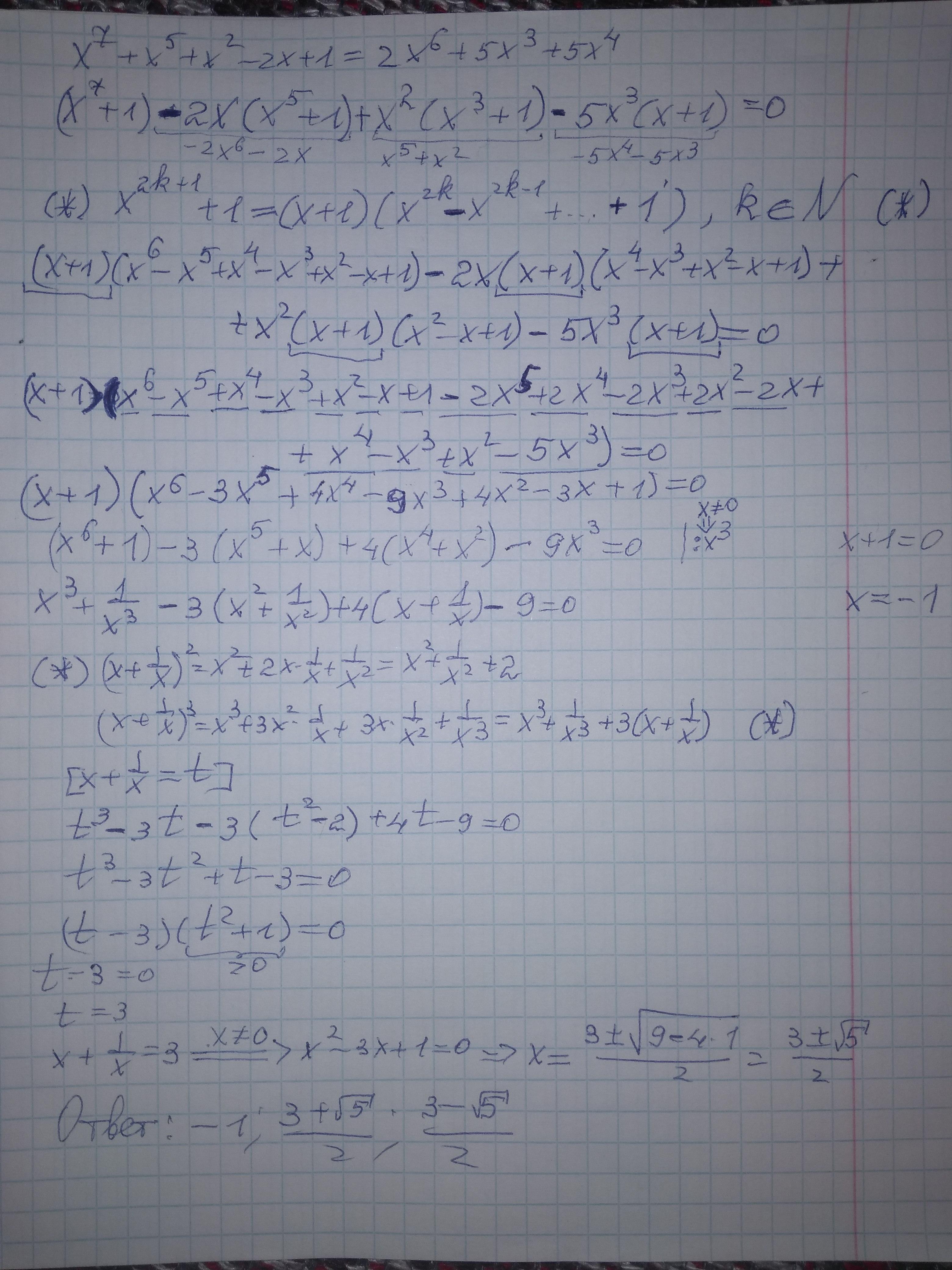
WhatYouNeed:
А как догадаться до замены t = x+(1/x) ?
Это ведь стандартный ход для симметрического уравнения
Симметрического четной степени*
К слову, исходное уравнение также симметрическое, но нечётной степени, а у них всегда одним из корней, очевидно, является -1 , и первым делом многочлен делят как раз на (x+1). Я как-то в принципе на это внимание не обратил, но на сложность и объем решения это не особо повлияло. Это просто альтернативное обоснование
Вас заинтересует
1 год назад
1 год назад
2 года назад
7 лет назад
8 лет назад