Помогите пожалуйста
Ответы
Ответ:
48
Объяснение:
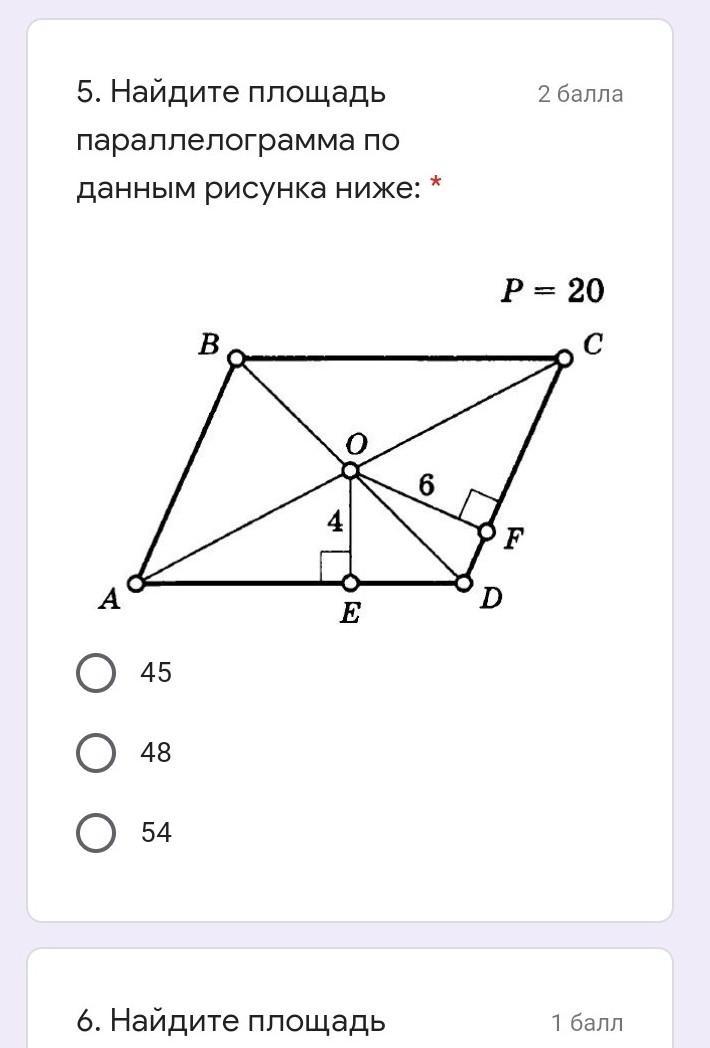
- Проводим линию OE и OF до конца и получаем конгруэнтные отрезки - высоты.
4×2=8 - высота, проведённая к основанию (сторона а)
6×2=12 - высота, проведённая к боковой стороне (b)
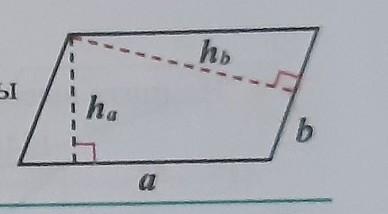
- Площадь параллелограмма находится по формуле: S=ah или S=bh (рисунок). То есть: 8а=12b. Сокращаем и получаем: 2а=3b
- Делим периметр на 2 и находим сумму a и b: 20:2=10 - сумма а и b
{ 2a=3b
{ a+b=10
{ 2а=3b
{ a=10-b
2(10-b)=3b
20-2b=3b
20=5b
b=4
a=10-4
a=6
a=6; b=4
8×6=48
12×4=48
Ответ:
48
Объяснение:
так как высоты в параллелограмме начинаются от середины пересечения диагоналей, то полная высота параллелограмма равна: 4×2=8 и 6×2=12.
Пусть одна сторона параллелограмма ВС=АД=х, а другая АВ=СД= у, и зная его периметр получим уравнение:
2х+2х=20
Площадь параллелограмма можно записать формулой: 8х и 12у. Поскольку площадь параллелограмма будет одинаковой в обоих случаях, запишем уравнение: 8х=12у. Составим систему уравнений:
2х+2у=20 |÷2
8х=12у |÷4
х+у=10
8х=12у
х=10-у
2х=3у
Подставим значение х во второе уравнение:
2(10-у)=3у
20–2у–3у=0
-5у= –20
у=(-20)÷(-5)
у=4
Итак: сторона АВ=СД=4
Теперь подставим значение у в первое уравнение:
х=10-у=10-4=6
Сторона ВС=АД=4.
Теперь найдём площадь параллелограмма по формуле: S=СД×2ОF=4×12=48(ед²); и второй вариант: S=АД×2ОЕ=6×8=48(ед²)